9.已知实数x,y满足$\left\{\begin{array}{l}x+y≥1\\ mx-y≤0\\ 2x-y+2≥0\end{array}\right.$,若z=3x-y的最大值为1,则m的值为( )
| A. | $\frac{8}{3}$ | B. | 2 | C. | 1 | D. | $\frac{2}{3}$ |
8.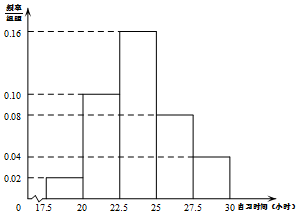 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )
 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )| A. | 26.25 | B. | 26.5 | C. | 26.75 | D. | 27 |
7.已知(1+x)n的展开式中第5项与第7项的二项式系数相等,则奇数项的二项式系数和为( )
| A. | 29 | B. | 210 | C. | 211 | D. | 212 |
5.对于函数y=f(x),若存在区间[a,b],当x∈[a,b]时的值域为[ka,kb](k>0),则称y=f(x)为k倍值函数.若f(x)=lnx+x是k倍值函数,则实数k的取值范围是( )
| A. | $({0,1+\frac{1}{e}})$ | B. | $({1,1+\frac{1}{e}})$ | C. | (1,1+e) | D. | (1,1+e2) |
3.我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积为“三斜公式”,设△ABC三个内角A,B,C所对的边分别为a,b,c,面积为S,则“三斜求积”公式为:S=$\sqrt{\frac{1}{4}[{a}^{2}{c}^{2}-(\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2})]}$,若a2sinC=4sinA,(a+c)2=12+b2,则用“三斜求积”公式求得△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{6}$ |
2.已知命题p:t=$\frac{π}{2}$,命题q:${∫}_{0}^{t}$sinxdx=1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.复数$\frac{2-3i}{3+2i}$+z对应的点的坐标为(2,-2),则z在复数平面内对应的点位于( )
0 239181 239189 239195 239199 239205 239207 239211 239217 239219 239225 239231 239235 239237 239241 239247 239249 239255 239259 239261 239265 239267 239271 239273 239275 239276 239277 239279 239280 239281 239283 239285 239289 239291 239295 239297 239301 239307 239309 239315 239319 239321 239325 239331 239337 239339 239345 239349 239351 239357 239361 239367 239375 266669
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |