题目内容
7.已知(1+x)n的展开式中第5项与第7项的二项式系数相等,则奇数项的二项式系数和为( )| A. | 29 | B. | 210 | C. | 211 | D. | 212 |
分析 直接利用二项式定理求出n,然后利用二项式定理系数的性质求出结果即可.
解答 解:已知(1+x)n的展开式中第5项与第7项的二项式系数相等,
可得Cn4=Cn6,可得n=4+6=10.
(1+x)10的展开式中奇数项的二项式系数和为:$\frac{1}{2}$×210=29.
故选:A.
点评 本题考查二项式定理的应用,组合数的形状的应用,考查基本知识的灵活运用以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知函数f(x)=2sin(ωx+φ)-1(ω>0,|φ|<π)的一个零点是$\frac{π}{3}$,函数y=f(x)图象的一条对称轴是x=-$\frac{π}{6}$,则ω取得最小值时,函数f(x)的单调区间是( )
| A. | [3kπ-$\frac{π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | B. | [3kπ-$\frac{5π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | ||
| C. | [2kπ-$\frac{2π}{3}$,2kπ-$\frac{π}{6}$],k∈Z | D. | [2kπ-$\frac{π}{3}$,2kπ-$\frac{π}{6}$],k∈Z |
15.已知命题p:若a,b是实数,则a>b是a2>b2的充分不必要条件;命题q:“?x∈R,x2+2>3x”的否定是“?x∈R,x2+2<3x”,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
2.已知命题p:t=$\frac{π}{2}$,命题q:${∫}_{0}^{t}$sinxdx=1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.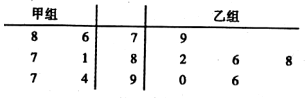 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
17.已知i为虚数单位,a∈R,$\frac{a-\sqrt{2}+i}{i}$为实数,则复数z=2a+$\sqrt{2}$i的模等于( )
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
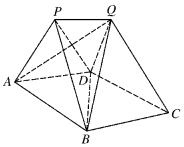 如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.
如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.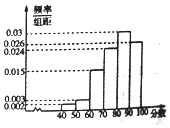 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:
2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: