题目内容

8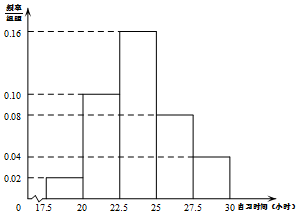．某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，若这200名学生中每周的自习时间不超过m小时的人数为164，则m的值约为（　　）
A．26.25B．26.5C．26.75D．27

分析 根据频率分布直方图，计算出每组的频率，再求出对应的频数，求出自习时间不超过m小时的频率为0.82，即可求出答案

解答 解：因为200名学生中每周的自习时间不超过m小时的人数为164，
则自习时间不超过m小时的频率为：$\frac{164}{200}$=0.82，
第一组的频率为0.05，第二组的频率为0.25，第三组的频率为0.4，第四组的频率为0.2，第五组的频率为0.1，
其中前三组的频率之和0.05+0.25+0.4=0.7，其中前四组的频率之和0.7+0.2=0.9，
则0.82落在第四组，m=25+$\frac{0.82-0.7}{0.2}$×2.5=26.5
故选：B．

点评 本题考查了频率分布直方图的应用问题，是基础题目．

练习册系列答案
相关题目
18．已知二次函数f（x）=x2+ax+b+1，关于x的不等式f（x）-（2b-1）x+b2＜1的解集为（b，b+1），其中b≠0．
（Ⅰ）求a的值；
（Ⅱ）令g（x）=$\frac{f（x）}{x-1}$，若函数φ（x）=g（x）-kln（x-1）存在极值点，求实数k的取值范围，并求出极值点．
19．$\frac{cos10°（1+\sqrt{3}tan10°）}{cos50°}$的值是2．
16．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{-x}+a，x≤0}\\{（x-1）^{3}+1，x＞0}\end{array}$，且?x0∈[2，+∞）使得f（-x0）=f（x0），若对任意的x∈R，f（x）＞b恒成立，则实数b的取值范围为（　　）
A．（-∞，0）B．（-∞，0]C．（-∞，a）D．（-∞，a]
3．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积为“三斜公式”，设△ABC三个内角A，B，C所对的边分别为a，b，c，面积为S，则“三斜求积”公式为：S=$\sqrt{\frac{1}{4}[{a}^{2}{c}^{2}-（\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}）]}$，若a2sinC=4sinA，（a+c）2=12+b2，则用“三斜求积”公式求得△ABC的面积为（　　）
A．$\sqrt{3}$B．2C．3D．$\sqrt{6}$
13．已知正项等差数列{an}的前n项和为Sn，S10=40，则a3•a8的最大值为（　　）
A．14B．16C．24D．40
20．如图1，在直角梯形ABCD中，AD∥BC，AD⊥DC，BC=2AD=2DC，四边形ABEF是正方形．将正方形ABEF沿AB折起到四边形ABE1F1的位置，使平面ABE1F1⊥平面ABCD，M为AF1的中点，如图2．

（I）求证：AC⊥BM；
（Ⅱ）求平面CE1M与平面ABE1F1所成锐二面角的余弦值．
17．已知函数f（x）=（ax-1）lnx+$\frac{x^2}{2}$．
（Ⅰ）若a=2，求曲线y=f（x）在点（1，f（1））处的切线l的方程；
（Ⅱ）设函数g（x）=f'（x）有两个极值点x1，x2，其中x1∈（0，e），求g（x1）-g（x2）的最小值．
18．某超市对某月（30天）每天顾客使用信用卡购物的人数进行了统计，得到如图所示的样本茎叶图，则该样本的中位数、众数、极差分别是（　　）
A．44，45，56B．44，43，56C．44，43，57D．45，43，57

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网