1.cos70°sin50°-cos200°sin40°的值为( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
20.已知集合A={x|x>1},B={y|y=x2,x∈R},则( )
| A. | A=B | B. | B?A | C. | A?B | D. | A∩B=∅ |
16.某商家在网上销售一种商品,从该商家的销售数据中抽取6天的价格与销量的对应数据,如下表所示:
(Ⅰ)由表中数据,看出可用线性回归模型拟合y与x的关系,试求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并预测当价格为1000元时,每天的商品的销量为多少;
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
15.某学校高一、高二、高三三个年级共有300名教师,为调查他们的备课时间情况,通过分层抽样获得了20名教师一周的备课时间,数据如下表(单位:小时):
(1)试估计该校高三年级的教师人数;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲,高二年级选出的人记为乙,假设所有教师的备课时间相对独立,求该周甲的备课时间不比乙的备课时间长的概率;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是8、9、10(单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为$\overline{x_1}$,表格中的数据平均数记为$\overline{x_0}$,试判断$\overline{x_0}$与$\overline{x_1}$的大小.(结论不要求证明)
| 高一年级 | 7 | 7.5 | 8 | 8.5 | 9 | |||
| 高二年级 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 高三年级 | 6 | 6.5 | 7 | 8.5 | 11 | 13.5 | 17 | 18.5 |
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲,高二年级选出的人记为乙,假设所有教师的备课时间相对独立,求该周甲的备课时间不比乙的备课时间长的概率;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是8、9、10(单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为$\overline{x_1}$,表格中的数据平均数记为$\overline{x_0}$,试判断$\overline{x_0}$与$\overline{x_1}$的大小.(结论不要求证明)
12.已知函数f(x)=x(a-$\frac{1}{e^x}$),曲线y=f(x)上存在两个不同点,使得曲线在这两点处的切线都与y轴垂直,则实数a的取值范围是( )
0 239149 239157 239163 239167 239173 239175 239179 239185 239187 239193 239199 239203 239205 239209 239215 239217 239223 239227 239229 239233 239235 239239 239241 239243 239244 239245 239247 239248 239249 239251 239253 239257 239259 239263 239265 239269 239275 239277 239283 239287 239289 239293 239299 239305 239307 239313 239317 239319 239325 239329 239335 239343 266669
| A. | (-e2,+∞) | B. | (-e2,0) | C. | (-$\frac{1}{e^2}$,+∞) | D. | (-$\frac{1}{e^2}$,0) |
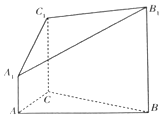 如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1
如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1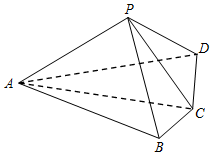 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.