题目内容
19．已知函数f（x）=alnx，g（x）=x+$\frac{1}{x}$+f′（x）（Ⅰ）讨论h（x）=g（x）-f（x）的单调性；
（Ⅱ）若h（x）的极值点为3，设方程f（x）+mx=0的两个根为x1，x2，且$\frac{{x}_{2}}{{x}_{1}}$≥ea，求证：$\frac{f′（{x}_{1}+{x}_{2}）+m}{f′（{x}_{1}-{x}_{2}）}$＞$\frac{6}{5}$．
分析 （Ⅰ）求出函数的导数，通过讨论a的范围求出函数的单调区间即可；
（Ⅱ）求出a的值，得到$\frac{f′{（x}_{1}{+x}_{2}）}{f′{（x}_{1}{-x}_{2}）}$=$\frac{1-\frac{{x}_{2}}{{x}_{1}}}{1+\frac{{x}_{2}}{{x}_{1}}}$+ln$\frac{{x}_{2}}{{x}_{1}}$，令$\frac{{x}_{2}}{{x}_{1}}$=t≥e2，根据函数的单调性证明即可．
解答 解：（Ⅰ）∵h（x）=g（x）-f（x）=x-alnx+$\frac{1+a}{x}$，其定义域是（0，+∞），
∴h′（x）=$\frac{（x+1）[x-（1+a）]}{{x}^{2}}$，
①1+a≤0即a≤-1时，x∈（0，+∞）时，h′（x）＞0，h（x）在（0，+∞）递增；
②a+1＞0即a＞-1时，x∈（0，1+a）时，h′（x）＜0，x∈（1+a，+∞）时，h′（x）＞0，
h（x）在（0，1+a）递减，在（1+a，+∞）递增，
综上，a＞-1时，h（x）在（0，1+a）递减，在（1+a，+∞）递增，
a≤-1时，h（x）在（0，+∞）递增；
（Ⅱ）由（Ⅰ）得x=1+a是函数h（x）的唯一极值点，故a=2；
∵2lnx1+mx1=0，2lnx2+mx2=0，
∴2（lnx2-lnx1）=m（x1-x2），
∴$\frac{f′{（x}_{1}{+x}_{2}）}{f′{（x}_{1}{-x}_{2}）}$=$\frac{{x}_{1}{-x}_{2}}{2}$（$\frac{2}{{x}_{1}{+x}_{2}}$+m）=$\frac{{x}_{1}{-x}_{2}}{{x}_{1}{+x}_{2}}$+m$\frac{{x}_{1}{-x}_{2}}{2}$=$\frac{1-\frac{{x}_{2}}{{x}_{1}}}{1+\frac{{x}_{2}}{{x}_{1}}}$+ln$\frac{{x}_{2}}{{x}_{1}}$，
令$\frac{{x}_{2}}{{x}_{1}}$=t≥e2，φ（t）=$\frac{1-t}{1+t}$+lnt，则φ′（t）=$\frac{{t}^{2}+1}{{t（t+1）}^{2}}$＞0，
∴φ（t）在[e2，+∞）上递增，
φ（t）≥φ（e2）=1+$\frac{2}{{e}^{2}+1}$＞1+$\frac{2}{{3}^{2}+1}$=$\frac{6}{5}$，
故$\frac{f′（{x}_{1}+{x}_{2}）+m}{f′（{x}_{1}-{x}_{2}）}$＞$\frac{6}{5}$．
点评 本题考查了函数的单调性、极值问题，考查不等式的证明以及函数和方程思想，考查转化思想以及计算能力，是一道综合题．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象（部分）如图所示，则f（x）的解析式是（ ）| A． | f（x）=2sin（πx+$\frac{π}{6}$） | B． | f（x）=2sin（2πx+$\frac{π}{6}$） | C． | f（x）=2sin（πx+$\frac{π}{3}$） | D． | f（x）=2sin（2πx+$\frac{π}{3}$） |
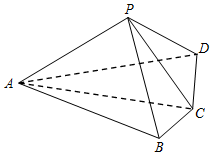如图，四棱锥P-ABCD中，平面PAC⊥平面ABCD，AC=2BC=2CD=4，∠ACB=∠ACD=60°．
