题目内容
15.某学校高一、高二、高三三个年级共有300名教师,为调查他们的备课时间情况,通过分层抽样获得了20名教师一周的备课时间,数据如下表(单位:小时):| 高一年级 | 7 | 7.5 | 8 | 8.5 | 9 | |||
| 高二年级 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 高三年级 | 6 | 6.5 | 7 | 8.5 | 11 | 13.5 | 17 | 18.5 |
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲,高二年级选出的人记为乙,假设所有教师的备课时间相对独立,求该周甲的备课时间不比乙的备课时间长的概率;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是8、9、10(单位:小时),这三个数据与表格中的数据构成的新样本的平均数记为$\overline{x_1}$,表格中的数据平均数记为$\overline{x_0}$,试判断$\overline{x_0}$与$\overline{x_1}$的大小.(结论不要求证明)
分析 (1)抽出的20位教师中,来自高三年级的有8名,根据分层抽样方法,能求出高三年级的教师共有多少人.
(2)从高一、高二年级分别抽取一人,共有35种基本结果,利用列举法求出该周甲的备课时间不比乙的备课时间长的基本结果种数,由此能求出该周甲的备课时间不比乙的备课时间长的概率.
(3)利用平均数定义能判断$\overline{x_0}$与$\overline{x_1}$的大小.
解答 解:(1)抽出的20位教师中,来自高三年级的有8名,
根据分层抽样方法,高三年级的教师共有300×$\frac{8}{20}$=120(人).
(2)从高一、高二年级分别抽取一人,共有35种基本结果,
其中甲该周备课时间比乙长的结果有:
(7.5,7),(8,7),(8.5,7),(8.5,8),(9,7),(9,8),共6种,
故该周甲的备课时间不比乙的备课时间长的基本结果有35-6=29种,
∴该周甲的备课时间不比乙的备课时间长的概率P=$\frac{29}{35}$.
(3)$\overline{x_1}$<$\overline{x_0}$.
点评 本题考查分层抽样、平均数的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
5.在△ABC中,a,b,c分别是角A、B、C所对的边长,A、B均为锐角,若sinA=cosB,则$\frac{a+b}{c}$的最大值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
20.已知集合A={x|x>1},B={y|y=x2,x∈R},则( )
| A. | A=B | B. | B?A | C. | A?B | D. | A∩B=∅ |
7.已知$α∈R,sinα+2cosα=\frac{{\sqrt{10}}}{2}$,则tan2α=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
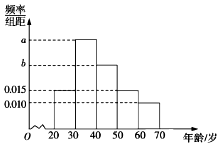 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.