题目内容
13.赌博有陷阱.某种赌博游戏每局的规则是:参与者现在从标有5、6、7、8、9的相同小球中随机摸取一个,将小球上的数字作为其赌金(单位:元);随后放回该小球,再随机摸取两个小球,将两个小球上数字之差的绝对值的2倍作为其资金(单位:元).若随机变量ξ和η分别表示参与者在每一局赌博游戏中的赌金与资金,则Eξ-Eη=3(元).分析 由题意可得:P(ξ=k)=$\frac{1}{5}$(k=5,6,7,8,9).可得Eξ=7.η的取值为:2,4,6,8.其中P(η=2)=$\frac{4}{{∁}_{5}^{2}}$,P(η=4)=$\frac{3}{{∁}_{5}^{2}}$,P(η=6)=$\frac{2}{{∁}_{5}^{2}}$,P(η=8)=$\frac{1}{{∁}_{5}^{2}}$,即可得出分布列与数学期望.
解答 解:由题意可得:P(ξ=k)=$\frac{1}{5}$(k=5,6,7,8,9).
可得Eξ=$\frac{5+6+7+8+9}{5}$=7.
η的取值为:2,4,6,8.其中P(η=2)=$\frac{4}{{∁}_{5}^{2}}$=$\frac{2}{5}$,
P(η=4)=$\frac{3}{{∁}_{5}^{2}}$=$\frac{3}{10}$,P(η=6)=$\frac{2}{{∁}_{5}^{2}}$=$\frac{1}{5}$,P(η=8)=$\frac{1}{{∁}_{5}^{2}}$=$\frac{1}{10}$,
其分布列为:
| η | 2 | 4 | 6 | 8 |
| P | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{1}{10}$ |
∴Eξ-Eη=7-4=3(元).
故答案为:3.
点评 本题考查了超几何分布列及其数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-2y+4≥0}\\{2x-y-4≤0}\end{array}\right.$,若x2+y2+2x≥k恒成立,则实数k的最大值为( )
| A. | 40 | B. | 9 | C. | 8 | D. | $\frac{7}{2}$ |
4.已知x,y∈R,( )
| A. | 若|x-y2|+|x2+y|≤1,则${(x+\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| B. | 若|x-y2|+|x2-y|≤1,则${(x-\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{3}{2}$ | |
| C. | 若|x+y2|+|x2-y|≤1,则${(x+\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ | |
| D. | 若|x+y2|+|x2+y|≤1,则${(x-\frac{1}{2})^2}+{(y+\frac{1}{2})^2}≤\frac{3}{2}$ |
8.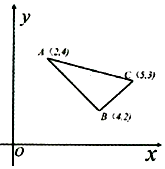 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | -1<a<1 | B. | -1≤a≤1 | C. | -1≤a<1 | D. | -1<a≤1 |
3.设Sn为等差数列{an}的前n项和,若a2017=S2017=2017,则首项a1=( )
| A. | -2014 | B. | -2015 | C. | -2016 | D. | -2017 |