7.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领到的钱数不少于其他任何人)的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |
6.已知命题p:对任意x∈R,总有2x>x2;q:“ab>4”是“a>2,b>2”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
5.若对于任意实数m∈[0,1],总存在唯一实数x∈[-1,1],使得m+x2ex-a=0成立,则实数a的取值范围是( )
| A. | [1,e] | B. | $({1+\frac{1}{e},e}]$ | C. | (0,e] | D. | $[{1+\frac{1}{e},e}]$ |
4.将函数y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数g(x)=sin2x的图象,当x1,x2满足时,|f(x1)-g(x2)|=2,${|{{x_1}-{x_2}}|_{min}}=\frac{π}{3}$,则φ的值为( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
3.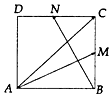 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | -1 |
2.已知等比数列{an}满足a1=$\frac{1}{2},{a_2}{a_8}=2{a_5}$+3,则a9=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{9}{8}$ | C. | 648 | D. | 18 |
19.某服装销售公司进行关于消费档次的调查,根据每人月均服装消费额将消费档次分为0-500元;500-1000元;1000-1500元;1500-2000元四个档次,针对A,B两类人群各抽取100人的样本进行统计分析,各档次人数统计结果如下表所示:
月均服装消费额不超过1000元的人群视为中低消费人群,超过1000元的视为中高收入人群.
(Ⅰ)从A类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从A,B两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计A,B两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
0 239050 239058 239064 239068 239074 239076 239080 239086 239088 239094 239100 239104 239106 239110 239116 239118 239124 239128 239130 239134 239136 239140 239142 239144 239145 239146 239148 239149 239150 239152 239154 239158 239160 239164 239166 239170 239176 239178 239184 239188 239190 239194 239200 239206 239208 239214 239218 239220 239226 239230 239236 239244 266669
| 档次 人群 | 0~ 500元 | 500~ 1000元 | 1000~ 1500元 | 1500~ 2000元 |
| A类 | 20 | 50 | 20 | 10 |
| B类 | 50 | 30 | 10 | 10 |
(Ⅰ)从A类样本中任选一人,求此人属于中低消费人群的概率;
(Ⅱ)从A,B两类人群中各任选一人,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(Ⅲ)以各消费档次的区间中点对应的数值为该档次的人均消费额,估计A,B两类人群哪类月均服装消费额的方差较大(直接写出结果,不必说明理由).
 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧面PDC⊥底面ABCD,△PDC是等边三角形,AB=AD=$\frac{1}{2}$CD=1,点E,F,G分别是棱PD,PC,BC的中点. 已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.
已知函数$f(x)=sin2x+sin(\frac{π}{3}-2x)$.