14.已知双曲线Γ:$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的上焦点为F1(0,c)(c>0),下焦点为F2(0,-c)(c>0),过点F1作圆x2+y2-$\frac{2c}{3}y+\frac{a^2}{9}$=0的切线与圆相切于点D,与双曲线下支交于点M,若MF2⊥MF1,则双曲线Γ的渐进线方程为( )
| A. | 4x±y=0 | B. | x±4y=0 | C. | 2x±y=0 | D. | x±2y=0 |
13.已知实数x,y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ \frac{x}{3}+\frac{y}{4}≤1\end{array}\right.$,则$\frac{y+1}{x+1}$的取值范围是( )
| A. | $[{-\frac{1}{6},5}]$ | B. | [1,5] | C. | $[{\frac{1}{4},5}]$ | D. | [0,5] |
12.已知cos(x-$\frac{π}{3}$)=$\frac{1}{3}$,则cos(2x-$\frac{2π}{3}$)+sin2($\frac{π}{3}$-x)的值为( )
| A. | $-\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{3}$ | D. | $-\frac{5}{3}$ |
8.已知直线a⊥平面α,则“直线b∥平面α”是“直线a⊥直线b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ex+m(m为常数),则f(m)=( )
| A. | e-1 | B. | 1-e | C. | $1-\frac{1}{e}$ | D. | $\frac{1}{e}-1$ |
6.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角等于( )
0 239021 239029 239035 239039 239045 239047 239051 239057 239059 239065 239071 239075 239077 239081 239087 239089 239095 239099 239101 239105 239107 239111 239113 239115 239116 239117 239119 239120 239121 239123 239125 239129 239131 239135 239137 239141 239147 239149 239155 239159 239161 239165 239171 239177 239179 239185 239189 239191 239197 239201 239207 239215 266669
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
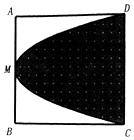 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.