题目内容
9.已知f(x)=ex(x2+x+1),定义f1(x)=f'(x),f2(x)=[f1(x)]′,…,fn+1(x)=[fn(x)]′,n∈N.经计算:f1(x)=ex(x2+3x+2);f2(x)=ex(x2+5x+5);f3(x)=ex(x2+7x+10),…照此规律,则fn(x)=fn(x)=ex[x2+(2n+1)x+n2+1].分析 根据题意,x的系数成等差数列,规律为2n+1,常数项为n2+1,即可得出结论.
解答 解:∵f1(x)=ex(x2+3x+2);f2(x)=ex(x2+5x+5);f3(x)=ex(x2+7x+10),…,
∴照此规律,fn(x)=ex[x2+(2n+1)x+n2+1],
故答案为fn(x)=ex[x2+(2n+1)x+n2+1].
点评 本题考查了导数的运算法则和归纳推理的问题,属于中档题.

练习册系列答案
相关题目
17.一组统计数据x1,x2,x3,x4,x5与另一组统计数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3相比较( )
| A. | 标准差相同 | B. | 中位数相同 | C. | 平均数相同 | D. | 以上都不相同 |
4.已知P={x|x2+2x-3<0},Q={-2,-1,0,1,2},则P∩Q=( )
| A. | {-1,0,1} | B. | {-2,-1,0,1} | C. | {-2,-1,0} | D. | {-1,0} |
14.已知双曲线Γ:$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的上焦点为F1(0,c)(c>0),下焦点为F2(0,-c)(c>0),过点F1作圆x2+y2-$\frac{2c}{3}y+\frac{a^2}{9}$=0的切线与圆相切于点D,与双曲线下支交于点M,若MF2⊥MF1,则双曲线Γ的渐进线方程为( )
| A. | 4x±y=0 | B. | x±4y=0 | C. | 2x±y=0 | D. | x±2y=0 |
1.已知约束条件为$\left\{\begin{array}{l}2x-y-6≤0\\ x-y+2≥0\end{array}\right.$,若目标函数z=kx+y仅在交点(8,10)处取得最小值,则k的取值范围为( )
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | (-∞,-2) | D. | (-1,+∞) |
19.已知$cos({\frac{2}{3}π-2θ})=-\frac{7}{9}$,则$sin({\frac{π}{6}+θ})$的值等于( )
| A. | $\frac{1}{3}$ | B. | $±\frac{1}{3}$ | C. | $-\frac{1}{9}$ | D. | $\frac{1}{9}$ |
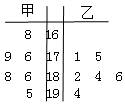 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: