题目内容
11.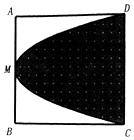 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为$\frac{2}{3}$.
分析 由题意,建立如图所示的坐标系,求出抛物线的方程,利用定积分求面积即可求出概率.
解答  解:由题意,建立如图所示的坐标系,则D(2,1),
解:由题意,建立如图所示的坐标系,则D(2,1),
设抛物线方程为y2=2px,代入D,可得p=$\frac{1}{4}$,∴y=$\sqrt{\frac{1}{2}x}$,
∴S=$2{∫}_{0}^{2}\sqrt{\frac{1}{2}x}dx$=$\sqrt{2}•\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{2}$=$\frac{8}{3}$,
∴点P恰好取自阴影部分的概率为$\frac{\frac{8}{3}}{4}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查利用定积分求面积,考查概率的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
1.若$\frac{a+i}{1+2i}=ti$(i为虚数单位,a,t∈R),则t+a等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
6.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角等于( )
| A. | $\frac{2π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
20.为调查我市居民对“文明出行”相关规定的了解情况,某媒体随机选取了30名行人进行问卷调查,将他们的年龄整理后分组,制成下表:
己知从中任选一人,年龄在(12,22]的频率为0.3
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
| 年龄(岁) | (12,22] | (22,32] | (32,42] | (42,52] | (52,62] | (62,72] |
| 频数 | m | 3 | 7 | 5 | 4 | n |
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
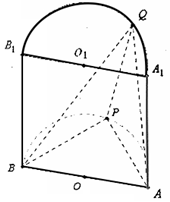 如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.
如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.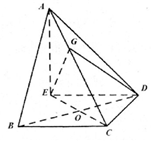 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.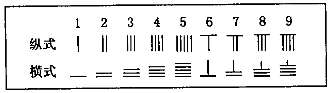
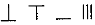 ,则5288用算筹式可表示为
,则5288用算筹式可表示为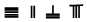 .
.