7.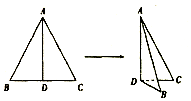 如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
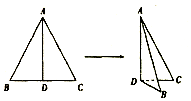 如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )| A. | $\frac{13}{2}π$ | B. | $\frac{13}{3}π$ | C. | $\frac{{13\sqrt{3}}}{2}π$ | D. | $\frac{{13\sqrt{3}}}{3}π$ |
6.点F1、F2分别是双曲线${x^2}-\frac{y^2}{3}=1$的左、右焦点,点P在双曲线上,则△PF1F2的内切圆半径r的取值范围是( )
| A. | $({0,\sqrt{3}})$ | B. | (0,2) | C. | $({0,\sqrt{2}})$ | D. | (0,1) |
5.已知B、C为单位圆上不重合的两定点,A为此单位圆上的动点,若点P满足$\overrightarrow{AP}=\overrightarrow{PB}+\overrightarrow{PC}$,则点P的轨迹为( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
4.如图,给出抛物线和其对称轴上的四个点P、Q、R、S,则抛物线的焦点是( )


| A. | P | B. | Q | C. | R | D. | S |
3.已知数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,数列{bn}的前n项和为${S_n}=\frac{{3{n^2}+7n}}{2}({n∈{N^*}})$,若这两个数列的公共项顺次构成一个新数列{cn},则满足cm<2012的m的最大整数值为( )
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
2.定义函数max$\left\{{f(x),g(x)}\right\}=\left\{{\begin{array}{l}{f(x)({f(x)≥g(x)})}\\{g(x)({f(x)<g(x)})}\end{array}}$,则max{sinx,cosx}的最小值为( )
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
1.点$({\sqrt{3},4})$在直线l:ax-y+1=0上,则直线l的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
20.“干支纪年法”是中国历法上自古以来就一直使用的纪年方法.干支是天干和地支的总称.甲、乙、丙、丁、戊、已、庚、辛、壬、癸十个符号叫天干,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个符号叫地支.把干支顺序相配正好六十为一周,周而复始,循环记录,这就是俗称的“干支表”.2016年是干支纪年法中的丙申年,那么2017年是干支纪年法中的( )
| A. | 丁酉年 | B. | 戊未年 | C. | 乙未年 | D. | 丁未年 |
19.已知集合A=N,B={x∈R|z=3+xi,且|z|=5}(i为虚数单位),则A∩B=( )
0 238928 238936 238942 238946 238952 238954 238958 238964 238966 238972 238978 238982 238984 238988 238994 238996 239002 239006 239008 239012 239014 239018 239020 239022 239023 239024 239026 239027 239028 239030 239032 239036 239038 239042 239044 239048 239054 239056 239062 239066 239068 239072 239078 239084 239086 239092 239096 239098 239104 239108 239114 239122 266669
| A. | 4 | B. | -4 | C. | {4} | D. | {-4} |