题目内容
3.已知数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,数列{bn}的前n项和为${S_n}=\frac{{3{n^2}+7n}}{2}({n∈{N^*}})$,若这两个数列的公共项顺次构成一个新数列{cn},则满足cm<2012的m的最大整数值为( )| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
分析 求出数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,数列{bn}的通项为bn=3n+2,从而得到cn=6n-1,由此能求出满足cm<2012的m的最大整数值.
解答 解:∵数列{an}的通项${a_n}=2n+3({n∈{N^*}})$,
数列{bn}的前n项和为${S_n}=\frac{{3{n^2}+7n}}{2}({n∈{N^*}})$,
∴${b}_{1}={S}_{1}=\frac{3+7}{2}$=5,
bn=Sn-Sn-1=3n+2,
n=1时,上式成立,∴bn=3n+2,
∵这两个数列的公共项顺次构成一个新数列{cn},
∴{cn}中的项分别为5,11,17,23,…,
∴cn=5+(n-1)×6=6n-1,
∵cm<2012,
∴cm=6m-1<2012,解得m<335$\frac{1}{2}$,
c335=6×335-1=2009,c336=6×336-1=2015,
∴满足cm<2012的m的最大整数值为335.
故选:A.
点评 本题考查满足条件的最大整数的求法,考查等差数列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
11.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角”.

该表由若干数字组成,从第二行起,每一行的数字均等于其“肩上”两数之和,表中最后一行今有一个数,则这个数为( )

该表由若干数字组成,从第二行起,每一行的数字均等于其“肩上”两数之和,表中最后一行今有一个数,则这个数为( )
| A. | 2017×22016 | B. | 2017×22014 | C. | 2016×22017 | D. | 2016×22018 |
13.将正奇数按如图所示的规律排列,则第21行从左向右的第5个数为( )


| A. | 731 | B. | 809 | C. | 852 | D. | 891 |
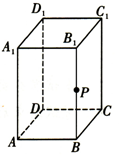 如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.
如图所示,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,P为棱BB1上的一个动点.