5.“五一”假期期间,某餐厅对选择A、B、C三种套餐的顾客进行优惠.对选择A、B套餐的顾客都优惠10元,对选择C套餐的顾客优惠20元.根据以往“五一”假期期间100名顾客对选择A、B、C三种套餐的情况得到下表:
将频率视为概率.
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量X表示两位顾客所得优惠金额的综合,求X的分布列和期望.
| 选择套餐种类 | A | B | C |
| 选择每种套餐的人数 | 50 | 25 | 25 |
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量X表示两位顾客所得优惠金额的综合,求X的分布列和期望.
1.已知命题p:将函数$f(x)=2sin({2x+\frac{π}{3}})$的图象向右平移$\frac{π}{4}$个单位,得到函数g(x)的图象,则函数g(x)在区间$[{-\frac{π}{3},0}]$上单调递增;命题q:定义在R上的函数y=f(x)满足f(-x)=f(3+x),则函数图象关于直线$x=\frac{3}{2}$对称,则正确的命题是( )
| A. | p∧q | B. | p∧(?q) | C. | (?p)∧(?q) | D. | (?p)∧q |
20.下列函数中不是奇函数的是( )
| A. | $y=\frac{{({{a^x}+1})x}}{{{a^x}-1}}({a>0,a≠1})$ | B. | $y=\frac{{{a^x}-{a^{-x}}}}{2}({a>0,a≠1})$ | ||
| C. | $y=\left\{\begin{array}{l}1,({x>0})\\-1,({x<0})\end{array}\right.$ | D. | $y={log_a}\frac{1+x}{1-x}({a>0,a≠1})$ |
19.若$z=\frac{3-i}{1+i}$(其中i是虚数单位),则|z+i|=( )
0 238926 238934 238940 238944 238950 238952 238956 238962 238964 238970 238976 238980 238982 238986 238992 238994 239000 239004 239006 239010 239012 239016 239018 239020 239021 239022 239024 239025 239026 239028 239030 239034 239036 239040 239042 239046 239052 239054 239060 239064 239066 239070 239076 239082 239084 239090 239094 239096 239102 239106 239112 239120 266669
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
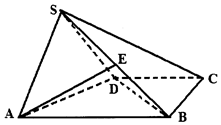 已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.
已知四棱锥S-ABCD中,底面是直角梯形,AB=2,BC=CD=1,BC⊥AB,侧面SAD是以∠ASD为直角的等腰三角形,且侧面SAD与底面ABCD垂直.