题目内容
4.在△ABC中,角A、B、C的对边分别为a、b、c,且$cos({A-\frac{π}{3}})=2cosA$.(1)若b=2,△ABC面积为$3\sqrt{3}$,求a;
(2)若$cos2C=1-\frac{a^2}{{6{b^2}}}$,求角B的大小.
分析 (1)先求出A,根据b=2,△ABC面积为$3\sqrt{3}$,利用三角形的面积公式、余弦定理求a;
(2)若$cos2C=1-\frac{a^2}{{6{b^2}}}$,得$tan2B=\frac{{\sqrt{3}}}{3}$,即可求角B的大小.
解答 解:(1)因为$cos({A-\frac{π}{3}})=2cosA$,
得$cosAcos\frac{π}{3}+sinAsin\frac{π}{3}=2cosA$,
即$sinA=\sqrt{3}cosA$,因为A∈(0,π),且cosA≠0,
所以$tanA=\sqrt{3}$,所以$A=\frac{π}{3}$.${S_{△ABC}}=\frac{1}{2}bcsinA=\frac{1}{2}×2c\frac{{\sqrt{3}}}{2}=3\sqrt{3}$,c=6,
由余弦定理${a^2}={b^2}+{c^2}-2bccosA={2^2}+{6^2}-2×2×6×\frac{1}{2}=28$,$a=2\sqrt{7}$.
(2)由$cos2C=1-\frac{a^2}{{6{b^2}}}$得$1-2cosC=2{sin^2}C=\frac{a^2}{{6{b^2}}}$,$sinC=\frac{a}{{2\sqrt{3}a}}=\frac{sinA}{{2\sqrt{2}sinB}}$,$sinBsinC=\frac{1}{4}$,$sinBsin({B+\frac{π}{3}})=\frac{1}{2}{sin^2}B+\frac{{\sqrt{3}}}{2}sinBcosB=\frac{1}{4}$,$\frac{1}{4}({1-cos2B})+\frac{{\sqrt{3}}}{4}sin2B=\frac{1}{4}$,$cos2B=\sqrt{3}sin2B$,
得$tan2B=\frac{{\sqrt{3}}}{3}$,
∵$2B∈({0,\frac{4π}{3}})$,∴$2B=\frac{π}{6}$或$2B=\frac{7π}{6}$得$B=\frac{π}{12}$或$B=\frac{7π}{12}$.
点评 本题考查三角形面积的计算,考查余弦定理,考查二倍角公式的运用,属于中档题.

| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 5 | D. | 2 |
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{5}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
| A. | $\frac{{\sqrt{26}}}{13}$ | B. | $\frac{{\sqrt{26}}}{26}$ | C. | 1 | D. | 2 |
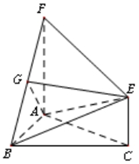 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF∥CE且AF=2CE,G是线段BF上一点,AB=AF=BC=2.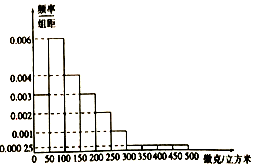 根据环境保护部《环境空气质量指数(AQI)技术规定》,空气质量指数(AQI)在201-300之间为重度污染;在301-500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
根据环境保护部《环境空气质量指数(AQI)技术规定》,空气质量指数(AQI)在201-300之间为重度污染;在301-500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.