8．
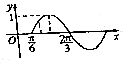函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，如果x1，x2∈（$\frac{π}{6}$，$\frac{2π}{3}$）且x1，x2是方程f（x）=m的两个实数根，其中m∈（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），则f（x1+x2）=（ ）
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，如果x1，x2∈（$\frac{π}{6}$，$\frac{2π}{3}$）且x1，x2是方程f（x）=m的两个实数根，其中m∈（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），则f（x1+x2）=（ ）| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
6．已知点F2，P分别为双曲线$\frac{{x}^{2}}{{a\;}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点与右支上的一点，O为坐标原点，若$\overrightarrow{OM}$=$\frac{1}{2}$（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$），${\overrightarrow{O{F}_{2}}}^{2}$=${\overrightarrow{{F}_{2}M}}^{2}$且2$\overrightarrow{O{F}_{2}}$•$\overrightarrow{{F}_{2}M}$=a2+b2，则该双曲线的离心率为（ ）
| A． | $\frac{\sqrt{3}+1}{2}$ | B． | $\frac{3}{2}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
5．已知圆O：x2+y2=r2，点P（a，b）（ab≠0）是圆O内一点，直线l的方程为ax+by+r2=0，那么（ ）
| A． | l与圆O相切 | B． | l与圆O相离 | ||
| C． | l与圆O相交 | D． | l与圆O相离或相切 |
4．若sin（$\frac{π}{4}$-α）=$\frac{3}{5}$，-$\frac{π}{4}$＜α＜0，则cos2α=（ ）
| A． | -$\frac{24}{25}$ | B． | $\frac{1}{5}$ | C． | -$\frac{1}{5}$ | D． | $\frac{24}{25}$ |
3．函数f（x）=-|x-1|，g（x）=x2-2x，定义$F（x）=\left\{\begin{array}{l}f（x），f（x）≥g（x）\\ g（x），f（x）＜g（x）\end{array}\right.$，则F（x）满足（ ）
| A． | 既有最大值，又有最小值 | B． | 只有最小值，没有最大值 | ||
| C． | 只有最大值，没有最小值 | D． | 既无最大值，也无最小值 |
2．下列说法正确的是（ ）
0 238910 238918 238924 238928 238934 238936 238940 238946 238948 238954 238960 238964 238966 238970 238976 238978 238984 238988 238990 238994 238996 239000 239002 239004 239005 239006 239008 239009 239010 239012 239014 239018 239020 239024 239026 239030 239036 239038 239044 239048 239050 239054 239060 239066 239068 239074 239078 239080 239086 239090 239096 239104 266669
| A． | “a＞b”是“a2＞b2”的充分不必要条件 | |
| B． | 命题“?x0∈R，$x_0^2+1＜0$”的否定是“?x∈R，x2+1＞0” | |
| C． | 关于x的方程x2+（a+1）x+a-2=0的两实根异号的充要条件是a＜1 | |
| D． | 命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为真命题 |