18.下列说法中正确的是( )
| A. | 若a>b,则ac2>bc2 | |
| B. | 若x≠0,则x+$\frac{4}{x}$的最小值为4 | |
| C. | “φ=$\frac{π}{2}$”是函数y=sin(x+φ)为偶函数“的充要条件 | |
| D. | 命题“?x>0,x-lnx>0”的否定是“?x0>0,x0-lnx0≤0” |
17.若一个底面是正三角形且侧棱垂直于底面的三棱柱的正(主)视图如图所示,则其侧面积等于( )


| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
16.i是虚数单位,复数$\frac{2-i}{1+i}$=( )
| A. | 1-3i | B. | 1+3i | C. | $\frac{1}{2}$-$\frac{3}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
15.已知集合A={x|x>1},B={x|(x+1)(x-2)<0},则A∪B=( )
| A. | {x|x>-1} | B. | {x|-1<x≤1} | C. | {x|-1<x<2} | D. | {x|1<x<2} |
14.汽车发动机排量可以分为两类,高于1.6L的称为大排量,否则称为小排量,加油时,有92号与95号两种汽油可供选择,某汽车网站的注册会员中,有300名老会员参与了网络调查,结果如下:
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据此次调查,是否有95%的把握认为该网站会员给汽车加油时进行的型号选择与汽车排量有关?
(2)将上述调查的频率视为概率,从该网站所有会员(数量最多)的“小排量汽车”和“大排量汽车”中分别抽出2辆,记X表示抽取的4辆中加95号汽油的车辆数,求X的分布列和期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| 加油类型 汽车排量 | 小排量 | 大排量 |
| 92号 | 160 | 96 |
| 95号 | 20 | 24 |
(2)将上述调查的频率视为概率,从该网站所有会员(数量最多)的“小排量汽车”和“大排量汽车”中分别抽出2辆,记X表示抽取的4辆中加95号汽油的车辆数,求X的分布列和期望.
13.设Sn为等差数列{an}的前n项和,若已知S6<S7,S7>S8,则下列叙述中正确的个数有( )
①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
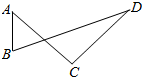
12.如图,A,B,C,D是平面上的任意四点,下列式子中正确的是( )
0 225109 225117 225123 225127 225133 225135 225139 225145 225147 225153 225159 225163 225165 225169 225175 225177 225183 225187 225189 225193 225195 225199 225201 225203 225204 225205 225207 225208 225209 225211 225213 225217 225219 225223 225225 225229 225235 225237 225243 225247 225249 225253 225259 225265 225267 225273 225277 225279 225285 225289 225295 225303 266669

| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{BC}$+$\overrightarrow{DA}$ | B. | $\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{AD}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{DB}$=$\overrightarrow{DC}$+$\overrightarrow{BA}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{DA}$=$\overrightarrow{AC}$+$\overrightarrow{DB}$ |
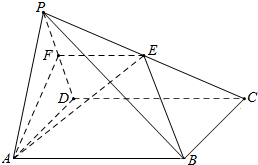 如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.