题目内容
11.若无穷等比数列{an}的各项和为3,则首项a1的取值范围为(0,3)∪(3,6).分析 依题意知|q|<1且q≠0,由$\underset{lim}{n→∞}$Sn=$\frac{{a}_{1}}{1-q}$=3⇒q=1-$\frac{{a}_{1}}{3}$∈(-1,1),从而可求得a1的取值范围.
解答 解:设等比数列的公比为q,
依题意知|q|<1且q≠0,
∴Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,
∴$\underset{lim}{n→∞}$Sn=$\frac{{a}_{1}}{1-q}$=3,
可得q=1-$\frac{{a}_{1}}{3}$∈(-1,1),
即-1<$\frac{{a}_{1}}{3}$-1<1且$\frac{{a}_{1}}{3}$-1≠0,
解得0<a1<3或3<a1<6.
故答案为:(0,3)∪(3,6).
点评 本题考查数列的求和与数列的极限,求得q=1-$\frac{{a}_{1}}{3}$是关键,考查转化思想与运算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
1.函数f(x)=log0.5(x-1)的定义域为( )
| A. | (-1,+∞) | B. | (1,+∞) | C. | (0,+∞) | D. | (-∞,0) |
16.i是虚数单位,复数$\frac{2-i}{1+i}$=( )
| A. | 1-3i | B. | 1+3i | C. | $\frac{1}{2}$-$\frac{3}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
20.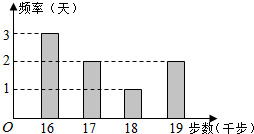 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.
 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:| 健步走步数(前步) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.
1.阅读如图所示的程序框图,若输入的k=10,那么输出的S值为( )


| A. | 1024 | B. | 2036 | C. | 1023 | D. | 511 |