3.过平面区域$\left\{\begin{array}{l}{x-y+2≥0}\\{y+2≥0}\\{x+y+2≤0}\end{array}\right.$内一点作圆O:x2+y2=1的两条切线,切点分别为A、B,记∠APB=α,则当α最小时,cosα的值为( )
| A. | $\frac{9}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{\sqrt{5}}{20}$ | D. | $\frac{4}{5}$ |
2.已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,a,b∈{1,2,3,4},则直线l1与直线l2没有公共点的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{16}$ |
1.已知集合M={x|x2-1≤0},N={x|-2<x<1,x∈Z},则M∩N( )
| A. | {-1,0} | B. | {1} | C. | {-1,0,1} | D. | ∅ |
19.生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计元件A,元件B为正品的概率;
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元.
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于300元的概率.
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元.
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于300元的概率.
15.设f(x)=log${\;}_{\frac{1}{2}}$x-ax>0在(0,$\frac{1}{4}$)上恒成立,a>0且a≠1,求a范围( )
0 225028 225036 225042 225046 225052 225054 225058 225064 225066 225072 225078 225082 225084 225088 225094 225096 225102 225106 225108 225112 225114 225118 225120 225122 225123 225124 225126 225127 225128 225130 225132 225136 225138 225142 225144 225148 225154 225156 225162 225166 225168 225172 225178 225184 225186 225192 225196 225198 225204 225208 225214 225222 266669
| A. | (1,+∞) | B. | (0,1) | C. | (0,1)∪(1,16] | D. | (1,16] |
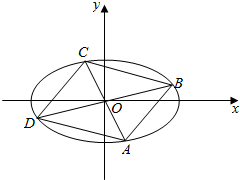 已知椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,短轴上端点为E,M(0,1)为线段OE的中点.
已知椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,短轴上端点为E,M(0,1)为线段OE的中点.