题目内容
2.已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,a,b∈{1,2,3,4},则直线l1与直线l2没有公共点的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{16}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件数是16,利用列举法写出满足条件的事件数,得到结果.
解答 解:直线l1的斜率${k_1}=\frac{1}{2}$,直线l2的斜率${k_2}=\frac{a}{b}$.
a,b∈{1,2,3,4}的总事件数为(1,1),(1,2),(1,3),(1,4),
(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),
(4,1),(4,2),(4,3),(4,4)共16种.
若直线l1与直线l2没有公共点,则l1∥l2,即k1=k2,即b=2a.
满足条件的实数对(a,b)有(1,2)、(2,4)、共2种情形.
∴对应的概率P=$\frac{2}{16}$=$\frac{1}{8}$.
故选:C
点评 本题考查等可能事件的概率,考查两条直线的平行关系,利用列举法是解决本题的关键.

练习册系列答案
相关题目
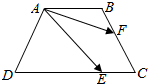 如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.
如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.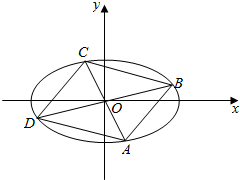 已知椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,短轴上端点为E,M(0,1)为线段OE的中点.
已知椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,短轴上端点为E,M(0,1)为线段OE的中点.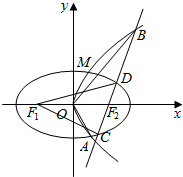 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和抛物线C2:y2=2px(p>0)都经过点M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),且椭圆C1的右焦点和抛物线C2的焦点F2相同.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和抛物线C2:y2=2px(p>0)都经过点M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),且椭圆C1的右焦点和抛物线C2的焦点F2相同.