2.定义在R的奇函数f(x),当x∈(-∞,0)时,f(x)+xf′(x)<0恒成立,若a=(log3π)•f(log3π),b=(logπ3)•f(logπ3),c=(-lnπ)•f(-lnπ),则( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
18.已知数列{an}满足a1=4,a2=2,a3=1,且数列{an+1-an}为等差数列,则数列{an}的通项公式为( )
0 224921 224929 224935 224939 224945 224947 224951 224957 224959 224965 224971 224975 224977 224981 224987 224989 224995 224999 225001 225005 225007 225011 225013 225015 225016 225017 225019 225020 225021 225023 225025 225029 225031 225035 225037 225041 225047 225049 225055 225059 225061 225065 225071 225077 225079 225085 225089 225091 225097 225101 225107 225115 266669
| A. | an=n-3 | B. | an=$\frac{1}{2}$(n3-8n2+13n+2) | ||
| C. | an=$\frac{1}{2}$(2n3-17n2+33n-10) | D. | an=$\frac{1}{2}$(n2-7n+14) |
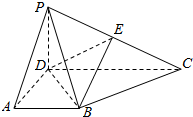 四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.
四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.