题目内容
20.若角α满足sinα-cosα=$\frac{\sqrt{2}}{2}$,则α=$\frac{5π}{12}+2kπ$或$\frac{13π}{12}+2kπ$,k∈Z.分析 由已知推导出sin($α-\frac{π}{4}$)=$\frac{1}{2}$,由此能求出α.
解答 解:∵sinα-cosα=$\frac{\sqrt{2}}{2}$,
∴$\sqrt{2}sin(α-\frac{π}{4})=\frac{\sqrt{2}}{2}$,
∴sin($α-\frac{π}{4}$)=$\frac{1}{2}$,
∴$α-\frac{π}{4}$=$\frac{π}{6}+2kπ$或$α-\frac{π}{4}$=$\frac{5π}{6}+2kπ$,k∈Z,
∴$α=\frac{5π}{12}+2kπ$或$α=\frac{13π}{12}+2kπ$,k∈Z.
故答案为:$\frac{5π}{12}+2kπ$或$\frac{13π}{12}+2kπ$,k∈Z.
点评 本题考查三角函数中角的求法,是基础题,解题时要认真审题,注意三角函数的性质的合理运用.

练习册系列答案
相关题目
15.已知集合A={x2-5x-6<0},B={x|2x<1},则图中阴影部分表示的集合是( )
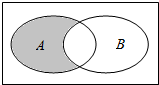

| A. | {x|2<x<3} | B. | {x|-1<x≤0} | C. | {x|0≤x<6} | D. | {x|x<-1} |