题目内容
5.已知实数x,y满足$\left\{\begin{array}{l}{4x-2y+1≥0}\\{x+y-2≤0}\\{x-4y-2≤0}\\{\;}\end{array}\right.$,则当$\frac{y+x}{x+1}$最小时,x=-$\frac{4}{7}$;y=-$\frac{9}{14}$.分析 由$\frac{y+x}{x+1}$=$\frac{x+1+y-1}{x+1}$=1+$\frac{y-1}{x+1}$,设k=$\frac{y-1}{x+1}$,利用k的几何意义,利用数形结合进行求解即可.
解答 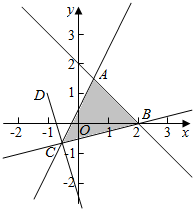 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
由$\frac{y+x}{x+1}$=$\frac{x+1+y-1}{x+1}$=1+$\frac{y-1}{x+1}$,
设k=$\frac{y-1}{x+1}$,则k的几何意义是区域内的点到定点(-1,1)的斜率,
由图象可知CD的斜率最小,
由$\left\{\begin{array}{l}{4x-2y+1=0}\\{x-4y-2=0}\end{array}\right.$得x=-$\frac{4}{7}$,y=-$\frac{9}{14}$,
故答案为:-$\frac{4}{7}$,-$\frac{9}{14}$.
点评 本题主要考查线性规划的应用,利用直线斜率和数形结合是解决本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
15.直线x+m2y+6=0与直线(m-2)x+3my+2m=0平行,则实数m的值为( )
| A. | m=0或m=3 | B. | m=-1或m=3 | C. | m=0或m=-1 | D. | m=-1 |
16.设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3,则方程f(x-1)=cosπx(-2≤x≤4)所有实根的和为( )
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
15.已知1gx=1.7,1gy=3.4,则下列选项中与lg(x2+2y)最接近的一个值为( )
| A. | 3.4 | B. | 3.9 | C. | 5.1 | D. | 7.1 |