题目内容
18.已知数列{an}满足a1=4,a2=2,a3=1,且数列{an+1-an}为等差数列,则数列{an}的通项公式为( )| A. | an=n-3 | B. | an=$\frac{1}{2}$(n3-8n2+13n+2) | ||
| C. | an=$\frac{1}{2}$(2n3-17n2+33n-10) | D. | an=$\frac{1}{2}$(n2-7n+14) |
分析 利用等差数列的通项公式及其前n项和公式、“累加求和”方法即可得出.
解答 解:设等差数列{an+1-an}的公差为d,
∵a1=4,a2=2,a3=1,
∴a2-a1=-2,a3-a2=-1,
∴d=-1-(-2)=1.
∴等差数列{an+1-an}的首项为-2,公差为1,
∴an+1-an=-2+(n-1)=n-3.
则an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(n-4)+(n-5)+…+(-2)+4
=$\frac{(n-1)(n-4-2)}{2}$+4
=$\frac{1}{2}({n}^{2}-7n+14)$.
故选:D.
点评 本题考查了等差数列的通项公式及其前n项和公式、“累加求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.己知抛物线x2=y上三点A,B,C,且A(-1,1),AB⊥BC,当点B移动时,点C的横坐标的取值范围是( )
| A. | (-∞,3]∪[1,+∞) | B. | (-∞,-2)∪(2,+∞) | C. | [1,+∞) | D. | [-3,1] |
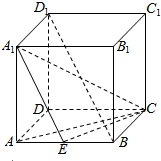 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.