6.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1,是否存在直线l,使其截双曲线所得弦的中点为P(1,1)?若存在,求出直线l的方程;若不存在,说明理由.
4.若抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )
0 224845 224853 224859 224863 224869 224871 224875 224881 224883 224889 224895 224899 224901 224905 224911 224913 224919 224923 224925 224929 224931 224935 224937 224939 224940 224941 224943 224944 224945 224947 224949 224953 224955 224959 224961 224965 224971 224973 224979 224983 224985 224989 224995 225001 225003 225009 225013 225015 225021 225025 225031 225039 266669
| A. | $\frac{{2+\sqrt{2}}}{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | $\frac{{1+\sqrt{2}}}{2}$ |
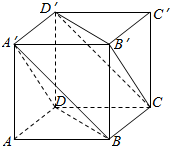 正方体ABCD-A′B′C′D′棱长为1
正方体ABCD-A′B′C′D′棱长为1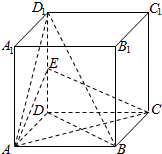 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点. 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.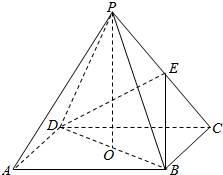 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.