若点A(1,0)和点B(4,0)到直线l的距离依次为1和2,则这样的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
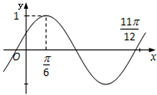 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、y=sin(2x+
| ||
B、y=sin(2x-
| ||
C、y=cos(2x+
| ||
D、y=cos(2x-
|
直线l:(2-m)x+(m+1)y-3=0与圆C:(x-2)2+(y-3)2=9的交点个数为( )
| A、2 | B、1 | C、0 | D、与m有关 |
以(-1,2)为圆心,
为半径的圆的方程为( )
| 5 |
| A、x2+y2-2x+4y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2+2x-4y=0 |
| D、x2+y2-2x-4y=0 |
已知定义域为R的函数y=f(x)在[0,7]上只有l和3两个零点,且y=f(2-x)与y=f (7+x)都是偶函数,则函数y=f(x)在[0,2013]上的零点个数为( )
| A、402 | B、403 |
| C、404 | D、405 |
已知向量
=(4-x,1),
=(y,x+5),x,y∈(0,+∞),且
⊥
,则xy取得最小值时,x=( )
| a |
| b |
| a |
| b |
| A、3 | ||
| B、1 | ||
| C、2 | ||
D、
|
已知全集为R,集合A={x|
≤1},B={x|-1≤x≤3},则A∩∁RB=( )
| 1 |
| x |
| A、(-1,3) |
| B、[-1,0]∪[1,3] |
| C、(-∞,-1)∪(3,+∞) |
| D、[1,3] |
用秦九韶算法求多项式f(x)=x6-5x5+6x4+x2+0.3x+2,在x=-2时,υ2的值为( )
| A、-161.7 | B、-40 |
| C、20 | D、81 |
直线在平面外是指( )
| A、直线与平面没有公共点 |
| B、直线与平面相交 |
| C、直线与平面平行 |
| D、直线与平面最多只有一个公共点 |