设双曲线F：
-
=1(a＞0，b＞0)，F1，F2为双曲线F的焦点．若双曲线F存在点M，满足
|MF1|=|MO|=|MF2|（O为原点），则双曲线F的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合S={x|x2-2x-3≤0}，T={x|-1＜x≤4，x∈Z}，则S∩T等于 （ ）
| A、{x|0＜x≤3，x∈Z} |
| B、{x|0≤x≤4，x∈Z} |
| C、{x|-1≤x≤0，x∈Z} |
| D、{x|-1＜x≤3，x∈Z} |
一名同学想要报考某大学，他必须从该校的7个不同的专业中选出5个，并按第一志愿，第二志愿，…，第五志愿顺序填进志愿表，若A专业不能作为第一志愿，B专业不能作为第二志愿，且A、B专业不能相邻，则不同的填法种数有（ ）
| A、1560 | B、1500 |
| C、1080 | D、960 |
已知偶函数f（x）在[0，+∞）上单调递减，则f（1）和f（-10）的大小关系为（ ）
| A、f（1）＞f（-10） |
| B、f（1）＜f（-10） |
| C、f（1）=f（-10） |
| D、f（1）和f（-10）关系不定 |
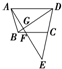如图，梯形ABCD中，E是DC延长线上一点，AE分别交BD于G，交BC于F．则下列结论：①
| EC |
| CD |
| EF |
| AF |
| FG |
| AG |
| BG |
| GD |
| AE |
| AG |
| BD |
| DG |
| AF |
| CD |
| AE |
| DE |
| A、1 | B、2 | C、3 | D、4 |
曲线y=-x2+1在点（1，0）处的切线方程为（ ）
| A、x+y-1=0 |
| B、2x-y-1=0 |
| C、2x+y-2=0 |
| D、x-y-1=0 |
已知AB是⊙O的切线，在下列条件中，能判定AB⊥CD的是（ ）
| A、AB与⊙O相切于点C，CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C，CD过圆心 |
| D、CD也是⊙O的切线 |
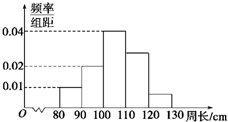为了解一片大约一万株树木的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出的样本频率分布直方图如图所示，那么在这片树木中，底部周长小于110cm的株数大约是（ ）| A、3000 | B、6000 |
| C、7000 | D、8000 |