题目内容
设双曲线F:
-
=1(a>0,b>0),F1,F2为双曲线F的焦点.若双曲线F存在点M,满足
|MF1|=|MO|=|MF2|(O为原点),则双曲线F的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题设条件结合双曲线性质推导出|MF1|=4a,|MO|=|MF2|=2a,取OF2的中点N,连结MN,得到MN⊥F1F2,且ON=
,F1N=
c,把x=
代入双曲线F,求出MN=
,由此能求出双曲线的离心率.
| c |
| 2 |
| 3 |
| 2 |
| c |
| 2 |
| b |
| 2a |
| c2-4a2 |
解答:
双曲线F存在点M,满足
|MF1|=|MO|=|MF2|(O为原点),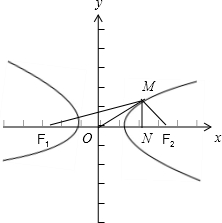
∴|MF1|=4a,|MO|=|MF2|=2a,
取OF2的中点N,连结MN,
则MN⊥F1F2,且ON=
,F1N=
c,
把x=
代入双曲线F,
得
-
=1,
解得MN=|y|=
,
∵|MF1|2=|F1N|2+|MN|2,
∴16a2=
c2+
(c2-4a2),
整理,得e4+4e2-60=0,
解得e2=6,或e2=-10(舍),
∴e=
.
故选:C.
| 1 |
| 2 |

∴|MF1|=4a,|MO|=|MF2|=2a,
取OF2的中点N,连结MN,
则MN⊥F1F2,且ON=
| c |
| 2 |
| 3 |
| 2 |
把x=
| c |
| 2 |
得
| c2 |
| 4a2 |
| y2 |
| b2 |
解得MN=|y|=
| b |
| 2a |
| c2-4a2 |
∵|MF1|2=|F1N|2+|MN|2,
∴16a2=
| 9 |
| 4 |
| b2 |
| 4a2 |
整理,得e4+4e2-60=0,
解得e2=6,或e2=-10(舍),
∴e=
| 6 |
故选:C.
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
长方体三个面的面对角线的长度分别为3,3,
那么它的外接球的表面积为( )
| 14 |
| A、8π | B、16π |
| C、32π | D、64π |
一个五位自然
,ai∈{0,1,2,3,4,5},i=1,2,3,4,5,当且仅当a1>a2>a3,a3<a4<a5时称为“凹数”(如32014,53134等),则满足条件的五位自然数中“凹数”的个数为( )
. |
| a1a2a3a4a5 |
| A、110 | B、137 |
| C、145 | D、146 |
已知函数f(x)=
,且关于x的方程f(x)-m=0,(m∈R)恰有三个互不相同的实数根x1,x2,x3,则x1x2x3的取值范围是( )
|
| A、(-4,0) | ||
B、(-
| ||
C、[-
| ||
| D、[-4,0) |