题目内容
曲线y=-x2+1在点（1，0）处的切线方程为（ ）
| A、x+y-1=0 |
| B、2x-y-1=0 |
| C、2x+y-2=0 |
| D、x-y-1=0 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到函数在x=1时的导数值，由直线方程的点斜式得切线方程．
解答：
解：由y=-x2+1，得y′=-2x，
∴y′|x=1=-2，
∴曲线y=-x2+1在点（1，0）处的切线的斜率为-2．
∴曲线y=-x2+1在点（1，0）处的切线方程为y-0=-2（x-1），即2x+y-2=0．
故选：C．
∴y′|x=1=-2，
∴曲线y=-x2+1在点（1，0）处的切线的斜率为-2．
∴曲线y=-x2+1在点（1，0）处的切线方程为y-0=-2（x-1），即2x+y-2=0．
故选：C．
点评：本题考查利用导数研究曲线上某点的切线方程，函数在曲线上某点处的导数，就是曲线在该点处的切线的斜率，是中档题．
练习册系列答案
相关题目
设F是双曲线
-
=1的右焦点，双曲线两渐近线分另．为l1，l2过F作直线l1的垂线，分别交l1，l2于A，B两点．若OA，AB，OB成等差数列，且向量
与
同向，则双曲线的离心 率e的大小为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| BF |
| FA |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
一个五位自然
，ai∈{0，1，2，3，4，5}，i=1，2，3，4，5，当且仅当a1＞a2＞a3，a3＜a4＜a5时称为“凹数”（如32014，53134等），则满足条件的五位自然数中“凹数”的个数为（ ）
. |
| a1a2a3a4a5 |
| A、110 | B、137 |
| C、145 | D、146 |
设集合S={x|x2-2x-3≤0}，T={x|-1＜x≤4，x∈Z}，则S∩T等于 （ ）
| A、{x|0＜x≤3，x∈Z} |
| B、{x|0≤x≤4，x∈Z} |
| C、{x|-1≤x≤0，x∈Z} |
| D、{x|-1＜x≤3，x∈Z} |
已知函数f(x)=
，且关于x的方程f（x）-m=0，（m∈R）恰有三个互不相同的实数根x1，x2，x3，则x1x2x3的取值范围是（ ）
|
| A、（-4，0） | ||
B、(-
| ||
C、[-
| ||
| D、[-4，0） |
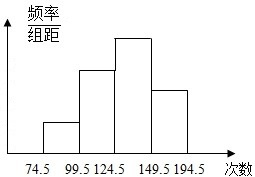为了解学生的体能情况，抽取了一个学校的部分学生进行一分钟跳绳次数测试，将所得数据整理成统计图如图，已知图中从左到右各个小组的高度之比分别为1：3：4：2，最左边一组的频数为5，请根据以上信息和图形解决以下问题：