已知函数f(x)=
x3+
ax2+bx+c在x1处取得极大值，在x2处取得最小值，满足x1∈（-1，1），x2∈（2，4），则a+2b的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、（-11，-3） |
| B、（-6，-4） |
| C、（-11，3） |
| D、（-16，-8） |
已知|
|=4，
为单位向量，当
，
的夹角为
时，
+
在
-
上的投影为（ ）
| a |
| e |
| a |
| e |
| 2π |
| 3 |
| a |
| e |
| a |
| e |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
长方体的一条对角线和同一顶点上的三条棱中的两条所成的角为60°、45°，则它和另一条棱所成的角为（ ）
| A、30° | B、60° |
| C、45° | D、不确定 |
已知m是一条直线，α，β是两个不同的平面，给出下列四个命题：
①若α⊥β，m?α，则m⊥β；
②若m?α，α∥β，则m∥β；
③若m∥α，m∥β，则α∥β；
④若m?α，m⊥β，则α⊥β．
其中正确的命题的序号是（ ）
①若α⊥β，m?α，则m⊥β；
②若m?α，α∥β，则m∥β；
③若m∥α，m∥β，则α∥β；
④若m?α，m⊥β，则α⊥β．
其中正确的命题的序号是（ ）
| A、①③ | B、② | C、①④ | D、②④ |
直线y-1=k（x-3）被圆（x-2）2+（y-2）2=4所截得的最短弦长等于（ ）
A、
| ||
B、2
| ||
C、2
| ||
D、
|
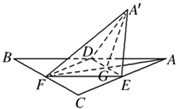如图，正△ABC的中线AF与中位线DE相交于G，已知△A′ED是△AED绕DE旋转过程中的一个图形．其中正确的说法是（ ）（1）动点A′在平面ABC上的射影在线段AF上
（2）恒有平面A′GF⊥平面BCED
（3）三棱锥A′-FED的体积有最大值
（4）异面直线A′E与BD不可能垂直．
| A、（1）（2）（3） |
| B、（1）（2）（4） |
| C、（2）（3）（4） |
| D、（1）（3）（4） |
已知f（x）为R上的可导函数，且满足f（x）＞f′（x），对任意正实数a，下面不等式恒成立的是（ ）
A、f(a)＞
| ||
B、f(a)＜
| ||
| C、f（a）＞eaf（0） | ||
| D、f（a）＜eaf（0） |
已知x，y满足约束条件
，则z=x+3y的最小值为（ ）
|
| A、1 | B、2 | C、3 | D、4 |