题目内容
设函数f(x)=
,其中a∈R
(1)解不等式f(x)≤-1;
(2)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数.
| ax-1 |
| x+1 |
(1)解不等式f(x)≤-1;
(2)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数.
考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)不等式f(x)≤-1,即
≤0,再分当a<-1时、当a=-1时、当a>-1三种情况,分别求得不等式解集.
(2)在(0,+∞)上任取x1<x2,化简f(x1)-f(x2)为
,显然只有当a+1<0时,才有
>0,函数f(x)在(0,+∞)上是减函数,由此求得a的范围.
| (a+1)x |
| x+1 |
(2)在(0,+∞)上任取x1<x2,化简f(x1)-f(x2)为
| (a+1)(x1-x2) |
| (x1+1)(x2+1) |
| (a+1)(x1-x2) |
| (x1+1)(x2+1) |
解答:
解:(1)不等式f(x)≤-1 即为
≤-1,即
≤0.
当a<-1时,不等式解集为(-∞,-1)∪[0,+∞);
当a=-1时,不等式解集为(-∞,-1)∪(-1,+∞);
当a>-1时,不等式解集为(-1,0].
(2)在(0,+∞)上任取x1<x2,
则 f(x1)-f(x2)=
-
=
.
由题设可得,x1-x2<0,x1+1>0,x2+1>0,
∴当a+1<0,即a<-1时,
>0,f(x1)-f(x2)>0,
函数f(x)在(0,+∞)上是减函数.
| ax-1 |
| x+1 |
| (a+1)x |
| x+1 |
当a<-1时,不等式解集为(-∞,-1)∪[0,+∞);
当a=-1时,不等式解集为(-∞,-1)∪(-1,+∞);
当a>-1时,不等式解集为(-1,0].
(2)在(0,+∞)上任取x1<x2,
则 f(x1)-f(x2)=
| ax1-1 |
| x1+1 |
| ax2-1 |
| x2+1 |
=
| (a+1)(x1-x2) |
| (x1+1)(x2+1) |
由题设可得,x1-x2<0,x1+1>0,x2+1>0,
∴当a+1<0,即a<-1时,
| (a+1)(x1-x2) |
| (x1+1)(x2+1) |
函数f(x)在(0,+∞)上是减函数.
点评:本题主要考查分式不等式的解法,函数的单调性的判断和证明,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
下列命题中,真命题是( )
| A、?x0∈R,|x0|≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a-b=0的充要条件是
| ||
| D、若p∧q为假,则p∨q为假(p,q是两个命题) |
执行如图所示的程序框图,输出的k值为( )


| A、3 | B、4 | C、5 | D、6 |
直线y-1=k(x-3)被圆(x-2)2+(y-2)2=4所截得的最短弦长等于( )
A、
| ||
B、2
| ||
C、2
| ||
D、
|
 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.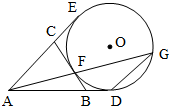 如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是
如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是