题目内容
已知x,y满足约束条件
,则z=x+3y的最小值为( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即看得到z的最小值.
解答:
解:作出不等式组对应的平面区域如图:
由z=x+3y得y=-
x+
z,
平移直线y=-
x+
z,
由图象可知当直线y=-
x+
z经过点A时,y=-
x+
z的截距最小,此时z最小.
由
,
解得
,即A(
,
),
代入z=x+3y=
+3×
=2.
即目标函数z=x+3y最小值为2.
故选:B.
由z=x+3y得y=-
| 1 |
| 3 |
| 1 |
| 3 |

平移直线y=-
| 1 |
| 3 |
| 1 |
| 3 |
由图象可知当直线y=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
由
|
解得
|
| 1 |
| 2 |
| 1 |
| 2 |
代入z=x+3y=
| 1 |
| 2 |
| 1 |
| 2 |
即目标函数z=x+3y最小值为2.
故选:B.
点评:本题主要考查线性规划的应用,利用z的几何意义结合数形结合,即可求出z的最小值.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
由200名学生的某次数学考试成绩绘制成了频率分布直方图(如图).由图可知在该次数学考试中成绩小于60分的学生数是( )


| A、600 | B、60 | C、40 | D、4 |
若曲线f(x)=xsinx+1在x=
处的切线与直线ax+2y+1=0互相垂直,则(ax2-
)5展开式中x的系数为( )
| π |
| 2 |
| 1 |
| x |
| A、40 | B、-10 |
| C、10 | D、-40 |
长方体的一条对角线和同一顶点上的三条棱中的两条所成的角为60°、45°,则它和另一条棱所成的角为( )
| A、30° | B、60° |
| C、45° | D、不确定 |
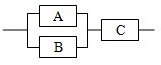 某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为
某个部件由三个元件如图方式连接而成,元件A或元件B正常工作,且元件C正常工作,则部件正常工作.若3个元件的次品率均为