题目内容
长方体的一条对角线和同一顶点上的三条棱中的两条所成的角为60°、45°,则它和另一条棱所成的角为( )
| A、30° | B、60° |
| C、45° | D、不确定 |
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:作出长方体,取对角线A1C,连接AC、D1C、B1C,不妨设对角线A1C与棱A1D1所成的角∠CA1D1=45°,对角线A1C与棱A1B1所成的角∠CA1B1=60°,设A1D1=a,由三角形的知识可表示出AC和A1C,由三角函数的定义可得所求角的正弦值,可得答案.
解答:
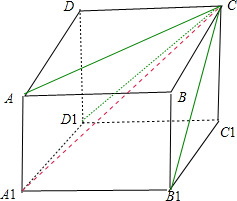 解:如图,取对角线为A1C,连接AC、D1C、B1C,
解:如图,取对角线为A1C,连接AC、D1C、B1C,
不妨设对角线A1C与棱A1D1所成的角∠CA1D1=45°,
对角线A1C与棱A1B1所成的角∠CA1B1=60°,
设A1D1=a,在RT△CA1D1中可得A1C=
a,
同理在RT△CA1B1中可得A1B1=
a,
可得AC=
=
a,
∴在△A1AC中,sin∠AA1C=
=
,
∴∠AA1C=60°,即该对角线和另一条棱所成的角为60°
故选:B
 解:如图,取对角线为A1C,连接AC、D1C、B1C,
解:如图,取对角线为A1C,连接AC、D1C、B1C,不妨设对角线A1C与棱A1D1所成的角∠CA1D1=45°,
对角线A1C与棱A1B1所成的角∠CA1B1=60°,
设A1D1=a,在RT△CA1D1中可得A1C=
| 2 |
同理在RT△CA1B1中可得A1B1=
| ||
| 2 |
可得AC=
a2+(
|
| ||
| 2 |
∴在△A1AC中,sin∠AA1C=
| AC |
| A1C |
| ||
| 2 |
∴∠AA1C=60°,即该对角线和另一条棱所成的角为60°
故选:B
点评:本题考查异面直线所成的角,涉及三角形的求解,属中档题.

练习册系列答案
相关题目
设等比数列{an}的前n项和为Sn,若Sm-1=5,Sm=-11,Sm+1=21,则m=( )
| A、3 | B、4 | C、5 | D、6 |
已知x,y满足约束条件
,则z=x+3y的最小值为( )
|
| A、1 | B、2 | C、3 | D、4 |
 某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.