题目内容
已知函数f(x)=
x3+
ax2+bx+c在x1处取得极大值,在x2处取得最小值,满足x1∈(-1,1),x2∈(2,4),则a+2b的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(-11,-3) |
| B、(-6,-4) |
| C、(-11,3) |
| D、(-16,-8) |
考点:简单线性规划,利用导数求闭区间上函数的最值
专题:导数的综合应用,不等式的解法及应用
分析:求函数的导数,根据函数极值和导数之间的关系,建立不等式组,利用线性规划的知识即可得到结论.
解答:
解:由题意得导函数f′(x)=x2+ax+b,
此函数图象开口向上,x1,x2为导函数图象与x轴的交点的横坐标,
又满足x1∈(-1,1),x2∈(2,4),
则有
,
那么点(a,b)所满足的平面区域如图所示为四边形ABCD内的部分(不包含边界),
令z=a+2b,易知点(a,b)为点A(-5,4)时,z有最大值3,
点(a,b)为点B(-3,-4)时,z有最小值-11,
所以a+2b的取值范围为(-11,3).
故选:C.
此函数图象开口向上,x1,x2为导函数图象与x轴的交点的横坐标,
又满足x1∈(-1,1),x2∈(2,4),
则有
|
那么点(a,b)所满足的平面区域如图所示为四边形ABCD内的部分(不包含边界),
令z=a+2b,易知点(a,b)为点A(-5,4)时,z有最大值3,
点(a,b)为点B(-3,-4)时,z有最小值-11,
所以a+2b的取值范围为(-11,3).

故选:C.
点评:本题主要考查函数的极值和导数之间的关系,以及一元二次方程根的发布,利用线性规划的知识求解是解决本题的关键.

练习册系列答案
相关题目
若曲线f(x)=xsinx+1在x=
处的切线与直线ax+2y+1=0互相垂直,则(ax2-
)5展开式中x的系数为( )
| π |
| 2 |
| 1 |
| x |
| A、40 | B、-10 |
| C、10 | D、-40 |
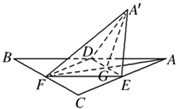 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形.其中正确的说法是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形.其中正确的说法是( )(1)动点A′在平面ABC上的射影在线段AF上
(2)恒有平面A′GF⊥平面BCED
(3)三棱锥A′-FED的体积有最大值
(4)异面直线A′E与BD不可能垂直.
| A、(1)(2)(3) |
| B、(1)(2)(4) |
| C、(2)(3)(4) |
| D、(1)(3)(4) |
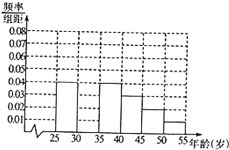 某同学在寒假期间进行社会实践活动,对[25,55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查,若生活习惯符合环保观念的称为“环保族”,否则称为“非环保族”,得到如下统计表和各年龄段人数的频率分布直方图:
某同学在寒假期间进行社会实践活动,对[25,55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查,若生活习惯符合环保观念的称为“环保族”,否则称为“非环保族”,得到如下统计表和各年龄段人数的频率分布直方图: