题目内容
已知m是一条直线,α,β是两个不同的平面,给出下列四个命题:
①若α⊥β,m?α,则m⊥β;
②若m?α,α∥β,则m∥β;
③若m∥α,m∥β,则α∥β;
④若m?α,m⊥β,则α⊥β.
其中正确的命题的序号是( )
①若α⊥β,m?α,则m⊥β;
②若m?α,α∥β,则m∥β;
③若m∥α,m∥β,则α∥β;
④若m?α,m⊥β,则α⊥β.
其中正确的命题的序号是( )
| A、①③ | B、② | C、①④ | D、②④ |
考点:命题的真假判断与应用,空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题:空间位置关系与距离
分析:①利用面面垂直的性质定理即可判断出;
②利用面面平行的性质定理即可判断出;
③利用线面面面平行的判定即可得出;
④利用面面垂直的判定定理即可判断出.
②利用面面平行的性质定理即可判断出;
③利用线面面面平行的判定即可得出;
④利用面面垂直的判定定理即可判断出.
解答:
解:①若α⊥β,m?α,则m与β不一定垂直,因此不正确;
②若m?α,α∥β,利用面面平行的性质定理可得m∥β,因此正确;
③若m∥α,m∥β,则α∥β或相交,因此不正确;
④若m?α,m⊥β,利用面面垂直的判定定理可得:α⊥β,因此正确.
综上可知:只有②④正确.
故选:D.
②若m?α,α∥β,利用面面平行的性质定理可得m∥β,因此正确;
③若m∥α,m∥β,则α∥β或相交,因此不正确;
④若m?α,m⊥β,利用面面垂直的判定定理可得:α⊥β,因此正确.
综上可知:只有②④正确.
故选:D.
点评:本题综合考查了线面面面平行与垂直的位置关系,属于基础题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


A、4
| ||||
B、
| ||||
C、
| ||||
| D、3 |
航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( )
| A、12种 | B、16种 |
| C、24种 | D、36种 |
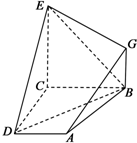 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=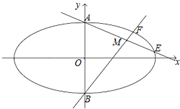 已知椭圆Γ:
已知椭圆Γ: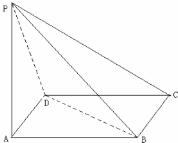 四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=
四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,∠BAD=60°,侧棱PA⊥平面ABCD,且PA=