设函数f(x)=|lg(x+1)|,满足f(a)=f(-
),f[10(a+1)+6(b+2)-1]=4lg2,其中a,b∈R,且a<b,则a+b的值为( )
| b+1 |
| b+2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、-1 |
要得到函数y=tan(2x+
)的图象,只须将y=tan2x的图象上的所有的点( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
设全集为R,集合M={x∈R|f(x)≠0},N={x∈R|g(x)≠0},则集合{x∈R|f(x)•g(x)=0}等于( )
| A、(∁RM)∩(∁RN) |
| B、(∁RM)∪(∁RN) |
| C、M∪(∁RN) |
| D、(∁RM)∪N |
已知函数f(x)=|lnx|,若
>a>b>1,则f(a),f(b),f(c)比较大小关系正确的是( )
| 1 |
| c |
| A、f(c)>f(b)>f(a) |
| B、f(b)>f(c)>f(a) |
| C、f(c)>f(a)>f(b) |
| D、f(b)>f(a)>f(c) |
已知函数f(x)=aln(x+1)-x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式
>1恒成立,则实数a的取值范围为( )
| f(p+1)-f(q+1) |
| p-q |
| A、[15,+∞) |
| B、(-∞,15] |
| C、(12,30] |
| D、(-12,15] |
在△ABC中,已知cos
=
,则cos
=( )
| A+B |
| 2 |
| 1 |
| 5 |
| C |
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
计算2cos215°-1的结果为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
命题p:若x<y,则|x|<|y|,命题q:若
>
,则a>b.则( )
| a |
| c2 |
| b |
| c2 |
| A、“p或q”为真 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p,q均为假 |
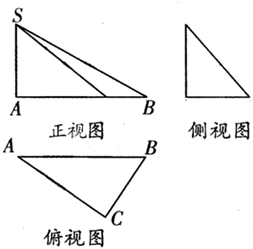 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
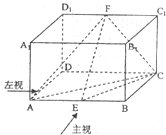 长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )
长方体ABCD-A1B1C1D1中,AA1=2,AD=3,AB=4,E,F分别在棱AB,C1D1上移动,则三棱锥F-AEC的主视图面积与左视图面积的比是( )