下列函数中，既是偶函数，又是在区间（0，+∞）上单调递减的函数是（　　）

某班级组织学生参加英语测试，成绩的频率分布直方图如图所示，若低于60分的人数是15人，则该班的学生人数是（　　）

已知圆C₁：x²+y²+4ax+4a²-4=0和圆C₂：x²+y²-2by+b²-1=0只有一条公切线，若a，b∈R且ab≠0，则

1

a2

+

1

b2

的最小值为（　　）

已知x，y满足

x+y-1≤0 x-y+1≥0 y≥-1

，且z=2x+y，则z的值域是（　　）

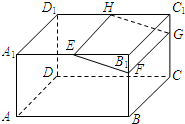如图，在长方体ABCD-A₁B₁C₁D₁中，E，H分别是棱A₁B₁，D₁C₁上的点（点E与B₁不重合），且EH∥A₁D₁，过EH的平面与棱BB₁，CC₁相交，交点分别为F，G．设AB=2AA₁=2a．在长方体ABCD-A₁B₁C₁D₁内随机选取一点，记该点取自于几何体A₁ABFE-D₁DCGH内的概率为P，当点E，F分别在棱A₁B₁，BB₁上运动且满足EF=a时，则P的最小值为（　　）

已知函数f（x）=cos（x+

π

2

）cosx（x∈R），则下面结论错误的是（　　）

已知

2y

x

+

8x

y

＞1+2m（x＞0，y＞0）恒成立，则实数m的取值范围是（　　）

若等比数列{a_n}满足2a₄=a₆-a₅，则q=（　　）

从1=1²，2+3+4=3²，3+4+5+6+7=5² 中可得到第n个式子的规律是（　　）

已知z=（1+i）（1-mi）是纯虚数（i是虚数单位），则实数m的值为（　　）