题目内容
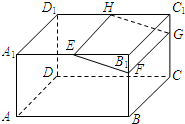 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据几何槪型的概率公式,结合基本不等式求出取自于几何体A1ABFE-D1DCGH内的概率为P的最小值,即可求出概率.
解答:
解:根据几何槪型的概率公式可知,点取自于几何体A1ABFE-D1DCGH内的概率为P=
,
∴若P的最小,则只需几何体A1ABFE-D1DCGH的体积最小,即五边形A1ABFE的面积最小,等价为三角形EFB1的面积最大,
∵EF=a,
∴B1E2+B1F2=a2,
则S △B1EF=
B1E•B1F≤
(B1E2+B1F2)=
,当且仅当B1F=B1E时取等号,
此时五边形A1ABFE的面积最小为2a2-
a2=
,
则取自于几何体A1ABFE-D1DCGH内的概率为P=
=
=
,
故选:D.
| VA1ABFE-D1DCGH |
| VABCD-A1B1C1D1 |
∴若P的最小,则只需几何体A1ABFE-D1DCGH的体积最小,即五边形A1ABFE的面积最小,等价为三角形EFB1的面积最大,
∵EF=a,
∴B1E2+B1F2=a2,
则S △B1EF=
| 1 |
| 2 |
| 1 |
| 4 |
| a2 |
| 4 |
此时五边形A1ABFE的面积最小为2a2-
| 1 |
| 4 |
| 7a2 |
| 4 |
则取自于几何体A1ABFE-D1DCGH内的概率为P=
| VA1ABFE-D1DCGH |
| VABCD-A1B1C1D1 |
| ||
| 2a2 |
| 7 |
| 8 |
故选:D.
点评:本题主要考查几何槪型的概率计算,根据体积槪型结合基本不等式求出最值是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
对a、b∈R,记max{a, b}=
,设f1(x)=|x-1|,f2(x)=-x2+6x-5,函数g(x)=max{f1(x),f2(x)},若方程g(x)=a有四个不同的实数解,则实数a的取值范围是( )
|
| A、[1,+∞) | ||
B、[
| ||
C、[
| ||
| D、(3,4) |
已知数列{an}首项为1,且满足an+1=
an,那么an等于( )
| n+1 |
| n |
| A、n | ||
| B、n+1 | ||
C、
| ||
D、
|
已知z=(1+i)(1-mi)是纯虚数(i是虚数单位),则实数m的值为( )
| A、±1 | B、1 | C、2 | D、-1 |
等差数列{an}中a1>0,S5=S8,则当Sn取最大值时n的值是( )
| A、6 | B、7 | C、6或7 | D、不存在 |
定义在(0,π)上的函数f(x)满足f′(x)•sinx<f(x)•cosx,则下列不等式正确的是( )
A、f(
| ||||||||
B、
| ||||||||
| C、sin2•f(1)<sin1•f(2) | ||||||||
D、sin1•f(
|
若数列{an}的前n项和Sn=3n2-10n,则数列的前10项中正数项的和为( )
| A、106 | B、208 |
| C、216 | D、118 |