已知F是抛物线y2=2x的焦点，A，B是该抛物线上的两点，|AF|+|BF|=3，则线段AB的中点到y轴的距离为（ ）
A、
| ||
| B、1 | ||
C、
| ||
D、
|
若函数f（x）=4sinωx•sin2（
+
）+cos2ωx（ω＞0）在[-
，
]上是增函数，则ω的取值范围是（ ）
| π |
| 4 |
| ωx |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| A、（0，1] | ||
B、（0，
| ||
| C、[1，+∞） | ||
D、[
|
已知f（x）的定义域为R，则p：?x∈R，（f（x）+f（-x））•（f（x）-f（-x））=0是q：f（x）为奇函数或偶函数的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
不等式
＞0的解集是（ ）
| x-2 |
| 1-x |
| A、{x|x＞2或x＜1} |
| B、{x|1＜x＜2} |
| C、{x|-1＜x＜2} |
| D、{x|x＞2或x＜-1} |
x＜0时，函数y=4x+
（ ）
| 1 |
| x |
| A、有最小值-4 |
| B、有最大值-4 |
| C、有最小值4 |
| D、有最大值4 |
如图所示的程序框图，若输入的n的值为1，则输出的k的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
若函数f（x）=ex-ax的一条切线经过原点，切点的纵坐标为e-1，则a的值是（ ）
| A、1 | ||
| B、e | ||
| C、-1 | ||
D、
|
一质点沿直线运动，若由始点起经过t秒后的位移为s=
t3+
t2-4t+7，那么速度为0的时刻为（ ）
| 1 |
| 3 |
| 3 |
| 2 |
| A、0秒 | B、1秒末 |
| C、2秒末 | D、1秒末和2秒末 |
在区间[-2，4]上随机地取一个数x，若x满足|x|≤m的概率为
，则实数m=（ ）
| 5 |
| 6 |
| A、1 | B、2 | C、3 | D、4 |
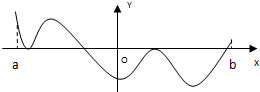函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值点（ ）| A、1个 | B、2个 | C、3个 | D、4个 |