已知i是虚数单位，则（1-i）（2+i）=（ ）
| A、-3-i | B、3-i |
| C、-3+i | D、3+i |
若双曲线x2+
=1的一条渐近线的倾斜角α∈（0，
），则m的取值范围是（ ）
| y2 |
| m |
| π |
| 3 |
| A、（-3，0） | ||||
B、（-
| ||||
| C、（0，3） | ||||
D、（-
|
数列{n2+n}中的项不能是（ ）
| A、380 | B、342 |
| C、321 | D、306 |
设函数f（x）=ax2+bx+c（a≠0），对任意实数t都有f（2+t）=f（2-t）成立，那么在函数值f（-1）、f（0）、f（2）、f（5）中，最小的一个不可能是（ ）
| A、f（5） | B、f（2） |
| C、f（-1） | D、f（1） |
用辗转相除法求49与91的最大公约数时的需要运算的次数为（ ）
| A、1次 | B、2次 | C、3次 | D、4次 |
过双曲线
-
=1（a＞0，b＞0）的左顶点A作与实轴垂直的直线，交两渐近线于M、N两点，F为该双曲线的右焦点，若△FMN的内切圆恰好是x2+y2=a2，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
若f（x）在x=x0处可导，则
（ ）
| lim |
| x→x0 |
| [f(x)]2-[f(x0)]2 |
| x-x0 |
| A、[f′（x0）]2 |
| B、2f′（x0）•f（x0） |
| C、f′（x0） |
| D、f（x0） |
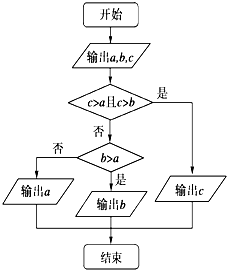如图程序框图表示的算法是（ ）| A、将a、b、c按从小到大输出 |
| B、将a、b、c按从大到小输出 |
| C、输出a、b、c三数中的最大数 |
| D、输出a、b、c三数中的最小数 |
（2x+a）5的展开式中，x2的系数等于40，则
（ex+2x）dx等于（ ）
| ∫ | a 0 |
| A、e | B、e-1 | C、1 | D、e+1 |