在空间直角坐标系中,点A的坐标(1,-2,3)且A与M关于x轴对称,则点M的坐标是( )
| A、(1,-2,-3) |
| B、(1,2,-3) |
| C、(1,2,3) |
| D、(-1,-2,3) |
函数f(x)=log2(1-3x)的值域为( )
| A、(0,+∞) |
| B、[0,+∞) |
| C、(-∞,0) |
| D、[-∞,0) |
先后抛掷一个质地均匀的骰子两次,其结果记为(a,b),其中a表示第一次抛掷的结果,b表示第二次抛掷的结果,则函数f(x)=x3+ax2+bx+c有极值点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线l过双曲线
-
=1的右焦点,斜率k=2.若l与双曲线的两个交点分别在左右两支上,则双曲线的离心率e的范围( )
| x2 |
| a2 |
| y2 |
| b2 |
A、e>
| ||
B、1<e<
| ||
C、1<e<
| ||
D、e>
|
函数f(x)=3x+5x的零点所在的区间是( )
A、(-1,-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
下列说法错误的是( )
| A、已知函数f(x)=ex+e-x,则f(x)是偶函数 | ||||||||
B、若非零向量
| ||||||||
| C、若命题p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0 | ||||||||
| D、若f′(x0)=0,则函数y=f(x)在x=x0处取得极值 |
与函数y=x相等的函数为( )
A、y=
| |||
B、y=(
| |||
C、y=
| |||
D、
|
向量
=(2,-3),
=(-1,λ),若
,
的夹角为钝角,则λ的取值范围为( )
| a |
| b |
| a |
| b |
A、λ>
| ||||
B、λ>
| ||||
C、λ>-
| ||||
D、λ>-
|




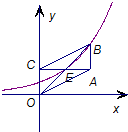 如图,面积为8的平行四边形OABC,对角线AC⊥CO,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1),经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥CO,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1),经过点E,B,则a=( )