题目内容
函数f(x)=3x+5x的零点所在的区间是( )
A、(-1,-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
考点:函数零点的判定定理
专题:常规题型
分析:由题意得,构造子函数,只要对应的函数值异号,由零点存在性定理即可解决问题.
解答:
解:设g(x)=3x,h(x)=-5x,
∵设g(-1)=
,h(-1)=5,
设g(-
)=
,h(-
)=
,
设g(-
)=
,h(-
)=
,
设g(-
)=
,h(-
)=1,
设g(0)=1,h(0)=0,
∴函数f(x)在区间(
,0)上必有零点.
故选:D
∵设g(-1)=
| 1 |
| 3 |
设g(-
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
设g(-
| 1 |
| 4 |
| 1 | ||
3
|
| 1 |
| 4 |
| 5 |
| 4 |
设g(-
| 1 |
| 5 |
| 1 | ||
3
|
| 1 |
| 5 |
设g(0)=1,h(0)=0,
∴函数f(x)在区间(
| 1 |
| 5 |
故选:D
点评:本题主要考查函数的零点及函数的零点存在性定理,函数的零点的研究就可转化为相应方程根的问题,函数与方程的思想得到了很好的体现.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
下面给出了四个式子,其中值为
的有( )
①
+
+
;
②
+
+
+
;
③
-
+
-
;
④
+
+
-
.
| 0 |
①
| AB |
| BC |
| CA |
②
| OA |
| OC |
| BO |
| CO |
③
| AB |
| AC |
| BD |
| CD |
④
| NQ |
| QP |
| MN |
| MP |
| A、①② | B、①③④ |
| C、①③ | D、①②③ |
直线l经过抛物线y2=4x的焦点,且与抛物线相交于A、B两点,若弦AB中点的横坐标为4,则|AB|=( )
| A、12 | B、10 | C、8 | D、6 |
已知圆O的半径为1,四边形ABCD为其内接正方形,EF为圆O的一条直径,M为正方形ABCD边界上一动点,则
•
的最小值为( )
| ME |
| MF |
A、-
| ||
B、-
| ||
C、-
| ||
| D、0 |
甲、乙、丙等6人排成一排,且甲、乙均在丙的同侧,则不同的排法共有( )种(用数字作答).
| A、720 | B、480 |
| C、144 | D、360 |
已知集合M={x||x-1|<2,x∈R},N={-1,0,1,2,3},则M∩N=( )
| A、{0,1,2} |
| B、{-1,0,1,2} |
| C、{-1,0,2,3} |
| D、{0,1,2,3} |
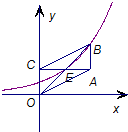 如图,面积为8的平行四边形OABC,对角线AC⊥CO,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1),经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥CO,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1),经过点E,B,则a=( )