函数f(x)=-
x3+x2+3x的单调递增区间为( )
| 1 |
| 3 |
| A、(-3,1) |
| B、(-1,3) |
| C、(-∞,-1)和(3,+∞) |
| D、(-∞,-3)和(1,+∞) |
在等差数列{an}中,a1+3a8+a15=120,则2a6-a4的值为( )
| A、24 | B、22 | C、20 | D、-8 |
如图程序框图是古代一数学家的算法程序框图,它输出的结果S代表( )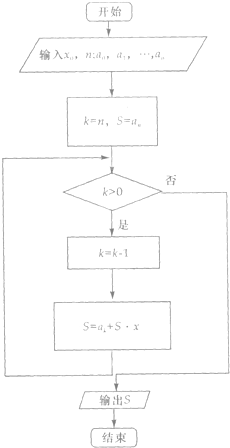

| A、一个数列的和 |
| B、一个n次多项式系数的和 |
| C、自变量取x.时,n次多项式函数的值 |
| D、自变量取x时,n个代数式的值 |
我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组解,二分法求函数零点等.对算法的描述有:
①对一类问题都有效;
②对个别问题有效;
③计算可以一步步地进行,每一步都有惟一的结果;
④是一种通法,只要按部就班地做,总能得到结果.
以上正确描述算法的有( )
①对一类问题都有效;
②对个别问题有效;
③计算可以一步步地进行,每一步都有惟一的结果;
④是一种通法,只要按部就班地做,总能得到结果.
以上正确描述算法的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知i为虚数单位,则 (1-i)2的值等于( )
| A、2-2i | B、2+2i |
| C、-2i | D、2i |
设f(x)=ln
,则F(x)=f(
)+f(
)的定义域为( )
| 2+x |
| 2-x |
| 2 |
| x |
| x |
| 2 |
| A、(-4,0)∪(1,4) |
| B、(-4,-1)∪(1,4) |
| C、(-4,0)∪(0,4) |
| D、(-4,-2)∪(2,4) |
和式
(yi+1)可表示为( )
| 5 |
 |
| i=1 |
| A、(y1+1)+(y5+1) |
| B、y1+y2+y3+y4+y5+1 |
| C、y1+y2+y3+y4+y5+5 |
| D、(y1+1)(y2+1)…(y5+1) |
若
<
<0,则下列结论不正确的是( )
| 1 |
| a |
| 1 |
| b |
A、
| ||||||
| B、a2>b2 | ||||||
| C、a3>b3 | ||||||
| D、|a|+|b|=|a+b| |
|
| A、充要 |
| B、必要不充分 |
| C、充分不必要 |
| D、既不充分也不必要 |
设a,b为两条直线,α,β为两个平面,下列说法正确的是( )
| A、若a?α,b?β,a∥b,则α∥β |
| B、若a、b是两条异面直线,且a∥α、a∥β,b∥α,b∥β,则α∥β |
| C、若a∥α,b?α,则a∥b |
| D、若a∥α,b∥β,α∥β,则a∥b |