题目内容
我们已学过的算法有求解一元二次方程的求根公式,加减消元法求二元一次方程组解,二分法求函数零点等.对算法的描述有:
①对一类问题都有效;
②对个别问题有效;
③计算可以一步步地进行,每一步都有惟一的结果;
④是一种通法,只要按部就班地做,总能得到结果.
以上正确描述算法的有( )
①对一类问题都有效;
②对个别问题有效;
③计算可以一步步地进行,每一步都有惟一的结果;
④是一种通法,只要按部就班地做,总能得到结果.
以上正确描述算法的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:算法和程序框图
分析:高中给的算法的描述性概念是:在数学上,算法通常是指按照一定规则解决某一类问题的明确的、有限的步骤.据此对每一个结论进行判断.
解答:
解:根据算法的概念容易判断①对;
②因为算法就是针对于某一类问题设计的,不会只能解决某一单独的、个别的问题,故②错;
由于算法是按照一定规则的、明确的、有限的步骤进行,并且每一步目的明确,因此③正确;
对于④,如果不能得到结果,算法就失去了意义,不能称之为算法了.
故①③④正确.
故选C
②因为算法就是针对于某一类问题设计的,不会只能解决某一单独的、个别的问题,故②错;
由于算法是按照一定规则的、明确的、有限的步骤进行,并且每一步目的明确,因此③正确;
对于④,如果不能得到结果,算法就失去了意义,不能称之为算法了.
故①③④正确.
故选C
点评:本题考查了算法的概念,必须结合实例反复体会,才能对算法概念有一个较为清晰地认识.

练习册系列答案
相关题目
已知集合A={x|x2-2x-3≤0},B={0,1,2,3,4},则A∩B=( )
| A、{1,2,3} |
| B、{0,1,2,3} |
| C、{-1,0,1,2,3} |
| D、{0,1,2} |
若函数f(x)=sin2x-
(x∈R),则f(x)是 ( )
| 1 |
| 2 |
A、最小正周期为
| ||
| B、最小正周期为π的奇函数 | ||
C、最小正周期为
| ||
| D、最小正周期为π的偶函数 |
|
| A、充要 |
| B、必要不充分 |
| C、充分不必要 |
| D、既不充分也不必要 |
若a<b<0下列不等式中不成立的是的是( )
| A、.|a|>|b| | ||||
B、
| ||||
C、
| ||||
| D、a2>b2 |
已知函数y=f(x)的图象如图所示,则下列说法中错误的是( )
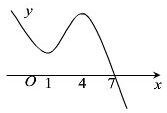

| A、f(x)在区间(-∞,1)上单调递减 |
| B、f(x)在区间(1,4)上单调递增 |
| C、当4<x<7时,f'(x)>0 |
| D、当x=1时,f'(x)=0 |
下列命题中正确的是( )
| A、函数y=48x-x3有两个极值点 |
| B、函数y=x3-x2+x有两个极值点 |
| C、函数y=x3有且只有1个极值点 |
| D、函数y=ex-x无极值点 |
已知x的不等式a(x-a)(x-
)>0,其中0<a<1,则它的解是( )
| 1 |
| a |
A、{x|x<a或x>
| ||
| B、{x|x>a} | ||
C、{x|x<
| ||
D、{x|x<
|