题目内容
函数f（x）=-
x3+x2+3x的单调递增区间为（ ）
| 1 |
| 3 |
| A、（-3，1） |
| B、（-1，3） |
| C、（-∞，-1）和（3，+∞） |
| D、（-∞，-3）和（1，+∞） |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：令f′（x）＞0，解出即可．
解答：
解：f′（x）=-x2+2x+3，
令f′（x）＞0，解得-1＜x＜3．
∴函数f（x）=-
x3+x2+3x的单调递增区间为（-1，3）．
故选：B．
令f′（x）＞0，解得-1＜x＜3．
∴函数f（x）=-
| 1 |
| 3 |
故选：B．
点评：本题考查了利用导数研究函数的单调性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的正视图为一个四边形，则这个几何体可能是下列几何体中的（ ）
①圆锥 ②圆柱 ③三棱锥 ④四棱柱．
①圆锥 ②圆柱 ③三棱锥 ④四棱柱．
| A、①② | B、②③ | C、①④ | D、②④ |
从分别写有ABCDE的5张卡片中任取两张，两字母恰好相连的概率（ ）
| A、0.2 | B、0.4 |
| C、0.3 | D、0.7 |
设f（x）=ln
，则F（x）=f（
）+f（
）的定义域为（ ）
| 2+x |
| 2-x |
| 2 |
| x |
| x |
| 2 |
| A、（-4，0）∪（1，4） |
| B、（-4，-1）∪（1，4） |
| C、（-4，0）∪（0，4） |
| D、（-4，-2）∪（2，4） |
△ABC中sin2A-sin2B-sin2C≥
sinBsinC时，角A的取值范围是（ ）
| 3 |
A、（0，
| ||
B、[
| ||
C、[
| ||
D、[0，
|
计箅cos42°cos18°-cos48°sin18°的结果等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
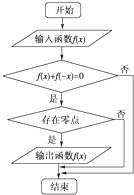
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
| A、f（x）=sinx | ||
| B、f（x）=cosx | ||
C、f（x）=
| ||
| D、f（x）=x2 |