两条平行直线和圆的位置关系定义为:若两条平行直线和圆有4个不同的公共点,则称两条平行直线和圆“相交”;若两条平行直线和圆没有公共点,则称两条平行直线和圆“相离”;若两条平行直线和圆有1个、2个或3个不同的公共点,则称两条平行直线和圆“相切”.已知直线l1:2x-y+a=0,l2:2x-y+a2+1=0和圆:x2+y2+2x-4=0相切,则a的取值范围是( )
A、-3≤a≤-
| ||||
B、a>
| ||||
| C、a>7或 a<-3 | ||||
| D、a≥7或 a≤-3 |
已知椭圆
+
=1上的点P到椭圆一个焦点的距离为7,则P到另一焦点的距离为( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、2 | B、3 | C、5 | D、7 |
若抛物线的顶点在原点,焦点与双曲线
-
=1的一个焦点重合,则该抛物线的标准方程可能是( )
| y2 |
| 4 |
| x2 |
| 5 |
| A、x2=4y |
| B、y2=4x |
| C、x2=-12y |
| D、y2=-12x |
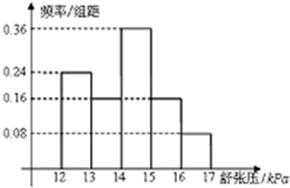 为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为
为研究某药物的疗效,选取若干志愿者进行临床研究所有志愿者舒张压数据(单位:kPa)的分组区[12,13),[13,14),[14,15﹚,[15,16﹚,[16,17﹚,将其从左到右的顺序分别编号为第一组,第二组,…第五组,如图是根据试验数据组成的频率分布直方图,已知第一组与第二组共20人,第三组中没有疗效的有6人,则第三组的人数为