题目内容
对于数列{un},若存在常数M>0对任意n∈N*恒有:|un+1-un|+|un-un-1|+…+|u2-u1|≤M,则称{un}是B-数列.
(1)首项为1,公比为-
的等比数列是否是B-数列?请说明理由.
(2)若数列{an}是B-数列,
①证明:{an2}也是B-数列;
②令An=
,求证:数列{An}是B-数列.
(1)首项为1,公比为-
| 1 |
| 2 |
(2)若数列{an}是B-数列,
①证明:{an2}也是B-数列;
②令An=
| a1+a2+…+an |
| n |
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:(1)设满足题设的等比数列为an,则an=(-
)n-1,于是|an-an-1|=
×(
)n-2(n≥2),由此可知首项为1,公比为-
的等比数列是B-数列;
(2)①证明|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2(M+|a1|)即可;
②证明|Ak-Ak+1|≤
(|a1-a2|+2|a2-a3|+…+k|ak-ak+1|),即可证明结论.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)①证明|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2(M+|a1|)即可;
②证明|Ak-Ak+1|≤
| 1 |
| k(k+1) |
解答:
解:(1)设满足题设的等比数列为an,则an=(-
)n-1.
于是|an-an-1|=
×(
)n-2(n≥2)
|an+1-an|+|an-an-1|+…+|a2-a1|=
[1+
+…+(
)n-1]=3×[1-(
)n]<3,
所以所以,该数列是B-数列;
(2)①:|an+1|≤|an+1-an|+|an-an-1|+…+|a2-a1|+|a1|≤M+|a1|,
∴|an+1|+|an|≤2(M+|a1|),
又|an+12-an2|≤[|an+1|+|an|]|an+1-an|≤2(M+|a1|)|an+1-an|可得
|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2(M+|a1|),
所以,{an2}也是B-数列;
②因为Ak=
,
所以|Ak-Ak+1|≤
(|a1-a2|+2|a2-a3|+…+k|ak-ak+1|),
∴
|Ak-Ak+1|≤|an+1-an|+|an-an-1|+…+|a2-a1|+|a1|≤M,
所以,数列{An}是B-数列.
| 1 |
| 2 |
于是|an-an-1|=
| 3 |
| 2 |
| 1 |
| 2 |
|an+1-an|+|an-an-1|+…+|a2-a1|=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以所以,该数列是B-数列;
(2)①:|an+1|≤|an+1-an|+|an-an-1|+…+|a2-a1|+|a1|≤M+|a1|,
∴|an+1|+|an|≤2(M+|a1|),
又|an+12-an2|≤[|an+1|+|an|]|an+1-an|≤2(M+|a1|)|an+1-an|可得
|an+12-an2|+|an2-an-12|+…+|a22-a12|≤2(M+|a1|),
所以,{an2}也是B-数列;
②因为Ak=
| a1+a2+…+ak |
| k |
所以|Ak-Ak+1|≤
| 1 |
| k(k+1) |
∴
| n |
 |
| k=1 |
所以,数列{An}是B-数列.
点评:本题考查数列的性质,考查学生分析解决问题的能力,有难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设x、y满足约束条件
,若x+2y≤a能成立,则a的取值范围为( )
|
| A、(-∞,1] |
| B、[1,+∞) |
| C、(-∞,7] |
| D、[7,+∞) |
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有4个不同的公共点,则称两条平行直线和圆“相交”;若两条平行直线和圆没有公共点,则称两条平行直线和圆“相离”;若两条平行直线和圆有1个、2个或3个不同的公共点,则称两条平行直线和圆“相切”.已知直线l1:2x-y+a=0,l2:2x-y+a2+1=0和圆:x2+y2+2x-4=0相切,则a的取值范围是( )
A、-3≤a≤-
| ||||
B、a>
| ||||
| C、a>7或 a<-3 | ||||
| D、a≥7或 a≤-3 |
已知点A在球O的表面上,过点A的作平面α,使OA与平面α成30°角,若平面α截球所得的圆面积为3π,则球O的体积为( )
A、
| ||
| B、4π | ||
C、
| ||
| D、16π |
计算:(log213)3+(log217)3+3log213log217=( )
| A、0 | B、1 | C、-1 | D、2 |
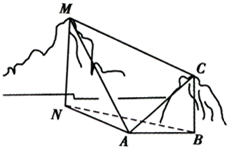 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,求山高MN.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,求山高MN.