已知|F1F2|=m,点P到两点F1、F2距离之差的绝对值为n(n<m).设点P的轨迹为C,过F1作AB⊥F1F2且交曲线C于点A、B,若△ABF2是直角三角形,则
的值为( )
| m |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
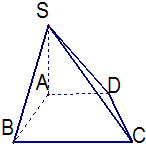 如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=
如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=| 3 |
| A、4π | B、5π | C、7π | D、8π |
| m |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=
如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=| 3 |
| A、4π | B、5π | C、7π | D、8π |