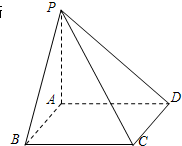
 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
三名男生和三名女生站成一排,若男生甲不站在两端,任意两名女生都不相邻,则不同的排列种数是( )
| A、120 | B、96 | C、84 | D、36 |
 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
| A、120 | B、96 | C、84 | D、36 |