题目内容
单摆从某点开始来回摆动,它相对于平衡位置O的位移S(厘米)和时间t(秒)的函数关系为:S=Asin(ωt+φ)(A>0,ω>0,0<φ<
),已知单摆每分钟摆动4次,它到平衡位置的最大位移为6厘米,摆动起始位置相对平衡位置的位移为3厘米.求:
(1)S和t的函数关系式;
(2)第2.5秒时单摆的位移.
| π |
| 2 |
(1)S和t的函数关系式;
(2)第2.5秒时单摆的位移.
考点:在实际问题中建立三角函数模型
专题:三角函数的图像与性质
分析:(1)利用已知条件求出函数的周期,振幅,利用函数的图象上的特殊点求出初相,即可得到S和t的函数关系式.
(2)代入t=2.5,求出S即可.
(2)代入t=2.5,求出S即可.
解答:
解:(1)单摆每分钟摆动4次,函数的周期为:25s.
=60,解得:ω=
,
它到平衡位置的最大位移为6厘米,A=6,
摆动起始位置相对平衡位置的位移为3厘米.说明函数的图象经过(0,3),
∴3=6sin(
×0+φ),(0<φ<
),∴φ=
.
S和t的函数关系式:S=6sin(
t+
).
(2)第2.5秒时单摆的位移S=6sin(
×2.5+
)=6×
=3
.
第2.5秒时单摆的位移为:3
.
| 2π |
| ω |
| π |
| 30 |
它到平衡位置的最大位移为6厘米,A=6,
摆动起始位置相对平衡位置的位移为3厘米.说明函数的图象经过(0,3),
∴3=6sin(
| π |
| 30 |
| π |
| 2 |
| π |
| 6 |
S和t的函数关系式:S=6sin(
| π |
| 30 |
| π |
| 6 |
(2)第2.5秒时单摆的位移S=6sin(
| π |
| 30 |
| π |
| 6 |
| ||
| 2 |
| 2 |
第2.5秒时单摆的位移为:3
| 2 |
点评:本题考查三角函数的解析式的求法与应用,考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
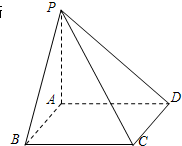 如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )
如图,已知四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为矩形,则下列结论中错误的是( )| A、平面PAB⊥平面PAD |
| B、平面PAB⊥平面PBC |
| C、平面PBC⊥平面PCD |
| D、平面PCD⊥平面PAD |
 已知定义在R上的奇函数f(x),当x∈(0,+∞)时的解析式为y=x2+2.
已知定义在R上的奇函数f(x),当x∈(0,+∞)时的解析式为y=x2+2. 如图所示为函数f(x)=2sin(ωx+φ)(
如图所示为函数f(x)=2sin(ωx+φ)(